PROGRAM LINEAR

Hana Fahira (14) XI IPS 2

Program linear adalah suatu metode penentuan nilai optimum dari suatu persoalan linear. Fyi, penyelesaian program linear dipakai untuk optimasi atau mencari nilai yang paling efektif dari suatu proses. Nilai optimum (maksimal atau minimum) diperoleh dari nilai dalam suatu himpunan penyelesaiaan persoalan linear. Di dalam persoalan linear terdapat fungsi linear yang bisa disebut sebagai fungsi objektif. Persyaratan, batasan, dan kendala dalam persoalan linear merupakan sistem pertidaksamaan linear.

Model Matematika Program Linear

Persoalan dalam program linear yang masih dinyatakan dalam kalimat-kalimat pernyataan umum, kemudian diubah kedalam model matematika. Model matematika merupakan pernyataan yang menggunakan peubah dan notasi matematika.

Sebagai ilustrasi, produsen sepatu membuat 2 model sepatu menggunakan 2 bahan yang berbeda. Komposisi model pertama terdiri dari 200 gr bahan pertama dan 150 gr bahan kedua. Sedangkan komposisi model kedua terdiri dari 180 gr bahan pertama dan 170 gr bahan kedua. Persediaan di gudang bahan pertama 72 kg dan bahan kedua 64 kg. Harga model pertama adalah Rp. 500.000,00 dan model kedua Rp. 400.000,00. Jika disimpulkan/disederhanakan dalam bentuk tabel menjadi berikut:

Dengan peubah dari jumlah optimal model 1 adalah x dan model 2 adalah y, dan hasil penjualan optimal adalah f(x, y) = 500.000x + 400.000y. Dengan syarat:

• Jumlah maksimal bahan 1 adalah 72.000 gr, maka 200x + 180y ≤ 72.000.
• Jumlah maksimal bahan 2 adalah 64.000 gr, maka 150x + 170y ≤ 64.000
• Masing-masing model harus terbuat.

Model matematika untuk mendapat jumlah penjualan yang maksimum adalah:

Maksimum f(x, y) = 500.000x + 400.000y

Syarat:

• 200x + 180y ≤ 72.000
• 150x + 170y ≤ 64.000
• x ≥ 0
• y ≥ 0

Nilai Optimum Fungsi Objektif

Fungsi objektif merupakan fungsi linear dan batasan-batasan pertidaksamaan linear yang memiliki himpunan penyelesaian. Himpunan penyelesaian yang ada merupakan titik-titik dalam diagram cartesius yang jika koordinatnya disubstitusikan kedalam fungsi linear dapat memenuhi persyaratan yang ditentukan.

Nilai optimum fungsi objektif dari suatu persoalan linear dapat ditentukan dengan metode grafik. Dengan melihat grafik dari fungsi objektif dan batasan-batasannya dapat ditentukan letak titik yang menjadi nilai optimum. Langkah-langkahnya sebagai berikut :

• Menggambar himpunan penyelesaian dari semua batasan syarat yang ada di cartesius.
• Menentukan titik-titik ekstrim yang merupakan perpotongan garis batasan dengan garis batasan yang lainnya. Titik-titik ekstrim tersebut merupakan himpunan penyelesaian dari batasannya dan memiliki kemungkinan besar membuat fungsi menjadi optimum.
• Menyelidiki nilai optimum fungsi objektif dengan dua acara yaitu :
  a. Menggunakan garis selidik
  b. Membandingkan nilai fungsi objektif tiap titik ekstrim

a. Menggunakan Garis Selidik

Garis selidik diperoleh dari fungsi objektif f(x, y) = ax + by dimana garis selidiknya adalah

ax + by = Z

Nilai Z diberikan sembarang nilai. Garis ini dibuat setelah grafik himpunan penyelesaian pertidaksamaan dibuat. Garis selidik awal dibuat di area himpunan penyelesaian awal. Kemudian dibuat garis-garis yang sejajar dengan garis selidik awal. Berikut pedoman untuk mempermudah penyelidikian nilai fungsi optimum:

Cara 1 (syarat a > 0)

• Jika maksimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di kiri garis tersebut. Titik yang dilalui garis tersebut adalah titik maksimum.

Jika minimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di kanan garis tersebut. Titik yang dilalui garis tersebut adalah titik minimum.

Cara 2 (syarat b > 0)

• Jika maksimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di bawah garis tersebut. Titik yang dilalui garis tersebut adalah titik maksimum.
• Jika minimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di atas garis tersebut. Titik yang dilalui garis tersebut adalah titik minimum.

Untuk nilai a < 0 dan b < 0 berlaku kebalikan dari kedua cara yang dijelaskan di atas.

b. Membandingkan Nilai Fungsi Tiap Titik Ekstrim

Menyelidiki nilai optimum dari fungsi objektif juga dapat dilakukan dengan terlebih dahulu menentukan titik-titik potong dari garis-garis batas yang ada. Titik-titip potong tersebut merupakan nilai ekstrim yang berpotensi memiliki nilai maksimum di salah satu titiknya.

Berdasarkan titik-titik tersebut ditentukan nilai masing-masing fungsinya, kemudian dibandingkan. Nilai terbesar merupakan nilai maksimum dan nilai terkecil merupakan nilai minimum.

             Contoh Soal Program Linear dan Pembahasan              

Contoh Soal 1

Tentukan nilai minimum f(x, y) = 9x + y pada daerah yang dibatasi oleh 2 ≤ x ≤ 6, dan 0 ≤ y ≤ 8 serta x + y ≤ 7.

Pembahasan:

• Langkah 1 menggambar grafiknya

• Langkah 2 menentukan titik ekstrim

Dari gambar, ada 4 titik ekstrim, yaitu: A, B, C, D dan himpunan penyelesaiannya ada di area yang diarsir.

• Langkah 3 menyelidiki nilai optimum

Dari grafik diketahui titik A dan B memiliki y = 0, sehingga kemungkinan menjadi nilai minimum. Kedua titik disubstitusikan kedalam f(x, y) = 9x + y untuk dibandingkan.

Dengan membandingkan, disimpulkan titik A memiliki nilai minimum 18

Contoh Soal 2

Tentukan dimana nilai maksimum fungsi f(x, y) = 4x + 5y yang akan dicapai pada pada grafik ini!

Titik ekstrim pada gambar adalah...

Pembahasan:

• A tidak mungkin maksimum karena titik paling kiri.
• B(3, 6)
• C(8, 2)
• D(8, 0)

Nilai tiap titik ekstrim adalah:

• 
• 
• 

Sehingga nilai maksimum ada pada titik yang melalui garis BC dengan nilai maksimum 42.

Contoh Soal 3

Pedagang buah memiliki modal Rp. 1.000.000,00 untuk membeli apel dan pisang untuk dijual kembali. Harga beli tiap kg apel Rp 4000,00 dan pisang Rp 1.600,00. Tempatnya hanya bisa menampung 400 kg buah. Tentukan jumlah apel dan pisang agar kapasitas maksimum.

Pembahasan:Diketahui:

Dengan syarat:

• Kapasitas tempat: x + y ≤ 400
• Modal: 4.000x + 1.600y ≤ 1.000.000 
• x ≥ 0
• y ≥ 0

Diagramnya:

Titik ekstrim:

• A(0, 400) bukan optimum karena tidak ada apel
• C(250, 0) bukan optimum karena tidak ada pisang
•  dengan metode eliminasi 2 persamaan diatas diperoleh:

Sehingga jumlah masimum:

• Apel: 150 kg
• Pisang: 250 kg

Contoh Soal 4

Perhatikan grafik di bawah ini.
Daerah penyelesaian dari sistem pertidaksamaan $3x+2y\le 36;x+2y\ge 20;x\ge 0$ dan $y\ge 0$

pada gambar di atas adalah ...

$\cdots \cdot$

Pembahasan:
$\mathrm{Grafik dari pertidaksamaan 3x+2y}\le 36$ memotong sumbu $X$ di $x=12$ dan memotong sumbu $Y$ di $y=18$. Karena bertanda $\le$, maka arsiran daerah penyelesaiannya ke bawah, yaitu daerah II, III, dan V. 
Grafik dari pertidaksamaan $x+2y\ge 20$ memotong sumbu $X$ di $x=20$ dan memotong sumbu $Y$ di $y=10$. Karena bertanda $\ge$, maka arsiran daerah penyelesaiannya ke atas, yaitu daerah I, II, dan V. 
$x,y$ juga bertanda nonnegatif. Ini berarti, daerah penyelesainnya hanya termuat di kuadran pertama. Dengan demikian, daerah penyelesaian sistem pertidaksamaan tersebut adalah daerah II.

Contoh Soal 5

Perhatikan gambar berikut!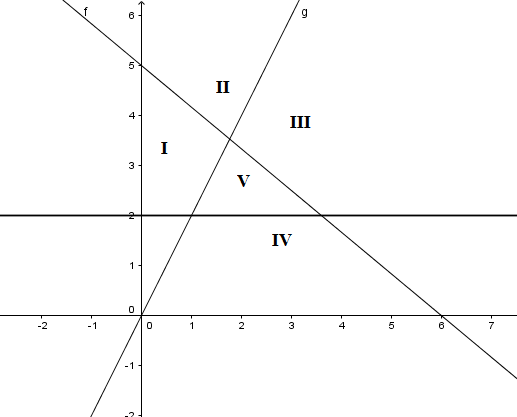
Daerah penyelesaian sistem pertidaksamaan $5x+6y\ge 30;-2x+y\le 0,y\ge 2$ ditunjukkan oleh daerah ...

Pembahasan:

Gambar garis $5x+6y\ge 30$ dengan memanfaatkan titik potong terhadap sumbu koordinat.
$\begin{array}{ccc}x& 0& 6\\ y& 5& 0\\ (x,y)& (0,5)& (6,0)\end{array}$
Jadi, garis melalui titik $(0,5)$ dan $(6,0)$. Uji titik $(0,0)$ pada $5x+6y\ge 30$, sehingga diperoleh $0+0=0\ge 30$ (bernilai salah), sehingga daerah penyelesaiannya tidak meliputi titik $(0,0)$.

Daerah penyelesaian meliputi daerah II dan III.
Selanjutnya, gambar garis $-2x+y\le 0$ dengan menentukan dua titik yang dilalui garis
$\begin{array}{ccc}x& 1& 2\\ y& 2& 4\\ (x,y)& (1,2)& (2,4)\end{array}$
Jadi, garis melalui titik $(1,2)$ dan $(2,4)$. Uji titik $(1,1)$ pada $-2x+y\le 0$, sehingga diperoleh $-2\left(1\right)+1=-1\le 0$ (bernilai benar), sehingga daerah penyelesaiannya meliputi titik $(1,1)$.

Daerah penyelesaian meliputi daerah III, IV, dan V.
Terakhir, gambarkan garis $y\ge 2$.

Daerah penyelesaian meliputi daerah I, II, III, dan V.
Daerah yang terkena ketiga arsiran daerah penyelesaian di atas adalah daerah III.

Contoh Soal 6

Perhatikan gambar berikut ini!

Nilai maksimum untuk fungsi objektif $P=3x+5y$ adalah ...

Pembahasan:
Daerah penyelesaian itu memiliki 3 titik pojok. Salah satunya adalah titik potong kedua garis itu. Koordinat titik potongnya dapat dicari dengan menggunakan metode penyelesaian SPLDV. Persamaan garis yang dimaksud dituliskan dalam sistem persamaan linear dua variabel berikut.

$\{\begin{array}{cc}5x+5y& =25\Rightarrow x+y=5\\ 3x+6y& =18\Rightarrow x+2y=6\end{array}$
Dengan menggunakan metode gabungan (eliminasi-substitusi) pada SPLDV, diperoleh
$\begin{array}{cc}& x+y=5\\ & x+2y=6\\ & -\\ & -y=-1\\ & y=1\end{array}$
Substitusikan $y=1$ pada persamaan pertama,
$\begin{array}{cc}x+y& =5\\ x+1& =5\\ x& =4\end{array}$
Jadi, titik potongnya ada di koordinat $(4,1)$.
Koordinat titik pojok daerah penyelesaian tersebut adalah $(0,3),(4,1)$, dan $(5,0)$. Uji titik ini pada fungsi objektif $P=3x+5y$.
$\begin{array}{cc}\text{Titik Pojok}& P=3x+5y\\ (0,3)& 15\\ (4,1)& 17\\ (5,0)& 15\end{array}$Dari tabel di atas, nilai maksimum fungsi objektif $P=3x+5y$ adalah 17

Contoh Soal 7

Umur pak Andi 28 tahun lebih tua dari umur Amira. Umur bu Andi 6 tahun lebih muda dari umur pak Andi. Jika jumlah umur pak Andi, bu Andi, dan Amira 119 tahun, maka jumlah umur Amira dan bu Andi adalah …. tahun

Pembahasan:

Misalkan Umur Pak Andi=x, umur Amira=y dan umur Ibu Andi=z

x = 28 + y (1)

z = x – 6; atau x=z+6 (2)

x + y + z = 119 (3)

dengan melakukan operasi penjumlahan (1) pada (2) didapatkan

2x = y + z + 34 atau 2x – y – z = 34 (4)

Lakukan operasi penambahan (3) pada (4) atau

x + y + z = 119

2x – y – z = 34

3x =153

Atau

x = 51

Dengan melakukan substitusi x pada (1) dan (2) didapatkan

Y = 23; z = 45

Sehingga, jumlah umur Amira (y) dan bu Andi (z) adalah y+z=23+45=68

Contoh Soal 8

Daerah yang diarsir pada gambar merupakan grafik himpunan penyelesaian sistem pertidaksamaan… 

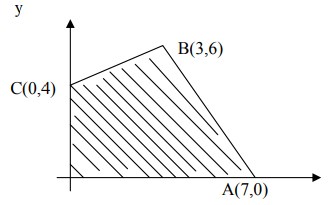Pembahasan:

Contoh Soal 9

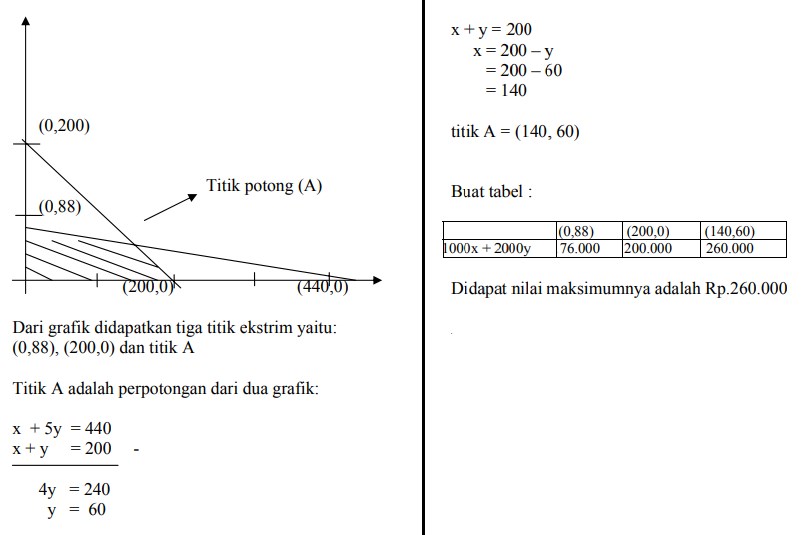
Luas daerah parkir 1.760 m² . Luas rata-rata untuk mobil kecil 4 m² dan mobil besar 20 m² . Daya tampung maksimum hanya 200 kendaraan, biaya parker mobil kecil Rp. 1000/jam dan mobil besar Rp.2000/jam. Jika dalam satu jam terisi penuh dan tidak ada kendaraan yang pergi dan dating, maka hasil maksimum tempat parkir itu adalah...

Pembahasan:

Dibuat persamaan-persamaannya terlebih dahulu:

Misal mobil kecil = x dan mobil besar = y

4 x + 20 y ≤ 1760

x + 5y ≤ 440 …..(1)

x + y ≤ 200 ….(2)

nilai maksimum 1000x + 2000y = ?

buat sketsa grafiknya:

Contoh Soal 10

Himpunan penyelesaian sistem pertidaksamaan

5x + y ≥ 10

2x + y ≤ 8

        y ≥ 2

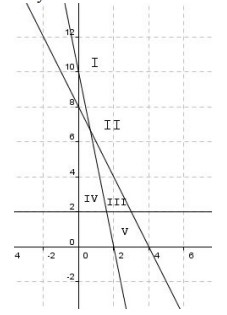
ditunjukkan oleh daerah . . .

Pembahasan:

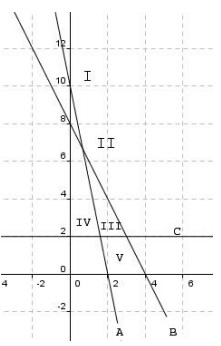
• Terlihat pada gambar bahwa A adalah persamaan garis 5x + y = 10 titik potong dengan sumbu x jika y = 0

x = 2 → titik (2,0)

titk potong dengan sumbu y jika x = 0

y = 10 → titik (0,10)

daerah 5x + y ≥ 10 berada pada garis persamaan tersebut dan di atas garis (I, II,III, V) —(a)

• B adalah persamaan garis 2x + y = 8 titik potong dengan sumbu x jika y=0 x = 4 → (4,0)

titik potong dengan sumbu y jika x = 0 y = 8 → (0,8)

daerah 2x + y ≤ 8 berada pada garis persamaan tersebut dan di bawah garis (III, V) ….(b)

•  C adalah garis y = 2

daerah di atas garis y = 2 adalah I, II, III, IV …(b)

dari (a) , (b) dan (c) :

• 1. I II III V
• 2. III V
• 3. I II III IV

Yang memenuhi ketiga-tiganya adalah daerah III.

     Sekian adalah materi dan contoh soal mengenai Program Linear yang telah saya jabarkan. Semoga dengan membaca blog ini dapat lebih memahami materi Program Linear.


Daftar Pustaka
Sumber : 
https://www.studiobelajar.com/program-linear/

https://idschool.net/sma/contoh-soal-dan-pembahasan-program-linear-matematika-sma/

https://mathcyber1997.com/soal-dan-pembahasan-program-linear-tingkat-sma-sederajat/

https://soalkimia.com/contoh-soal-program-linear/