LOGIKA MATEMATIKA

Hana Fahira | XI IPS 2

    Logika matematika merupakan salah satu materi dari induksi matematika. Logika matematika adalah cabang logika dan matematika yang mengandung kajian matematis logika dan aplikasi kajian ini pada bidang-bidang lain di luar matematika.. Hal-hal pada logika matematika yang akan kita pelajari kali ini antara lain mengenai pernyataan, ingkaran, hubungan antara dua kalimat atau lebih serta bagaimana menarik kesimpulan dari kalimat-kalimat yang diberikan.

    Pada dasarnya, pernyataan merupakan suatu kalimat yang bernilai benar ataupun salah, namun tidak keduanya. Sedangkan, suatu kalimat dikatakan bukan pernyataan jika kita tidak dapat menentukan apakah kalimat tersebut benar atau salah atau mengandung pengertian relatif. Di dalam logika matematika terdapat dua jenis pernyataan, yaitu pernyataan tertutup dan pernyataan terbuka. Pernyataan tertutup merupakan pernyataan yang sudah bisa dipastikan nilai kebenarannya sedangkan pernyataan terbuka yaitu pernyataan yang belum bisa dipastikan nilai kebenarannya.

Contoh:

• 8 + 2 = 10 (pernyataan tertutup yang bernilai benar)
• 4 × 6 = 20 (pernyataan tertutup yang bernilai salah)
• 5a + 10 = 40 (pernyataan terbuka, karena harus dibuktikan kebenarannya)
• Jarak Jakarta-Bogor adalah dekat (bukan pernyataan, karena dekat itu relatif)

Ingkaran/Negasi (~)

Ingkaran didefinisikan sebagai sebuah pernyataan yang memiliki nilai kebenaran yang berlawanan dengan pernyataan semula. Berikut adalah tabel kebenaran ingkaran.

p	~p
B	S
S	B

Artinya, jika suatu pertanyaan (p) bernilai benar (B), maka ingkaran (q) akan bernilai salah (S). Begitu pula sebaliknya.

Contoh:

p : Semua murid lulus ujian

~p : Ada murid yang tidak lulus ujian

Pernyataan Majemuk

Pernyataan majemuk merupakan pernyataan gabungan dari beberapa pernyataan tunggal yang dihubungkan dengan kata hubung. Pernyataan majemuk di dalam logika matematika terdiri dari disjungsi , konjungsi , implikasi , dan biimplikasi.

• Konjungsi (∧)

Suatu pernyataan p dan q dapat digabungkan dengan menggunakan kata hubung ‘dan’ sehingga membentuk pernyataan majemuk ‘p dan q’ yang disebut konjungsi yang dilambangkan dengan “p∧q”. Berikut adalah tabel kebenaran konjungsi.

p	q	p∧q
B	B	B
B	S	S
S	B	S
S	S	S

Dari tabel diatas dapat disimpulkan bahwa dalam konsep konjungsi akan bernilai benar jika dan hanya jika kedua pernyataan (p dan q) benar

Contoh:

Budi sudah makan belajar dan makan

Misalkan, untuk dapat diizinkan bermain oleh Ibu, Budi harus memenuhi kondisi di atas. Jika satu saja atau bahkan kedua pernyataan tersebut dilanggar, maka Budi tidak diizinkan untuk bermain.

• Disjungsi

Suatu pernyataan p dan q dapat digabungkan dengan menggunakan kata hubung ‘atau’ sehingga membentuk pernyataan majemuk ‘p atau q’ yang disebut disjungsi yang dilambangkan dengan “p ∨ q”. Berikut adalah tabel kebenaran disjungsi.

p	q	p∨q
B	B	B
B	S	B
S	B	B
S	S	S

Dari tabel diatas dapat disimpulkan bahwa dalam konsep disjungsi hanya akan bernilai salah jika kedua pernyataan (p dan q) salah.

Contoh:

Bandung atau Palembang adalah kota yang terletak di Pulau Jawa

Pernyataan Bandung adalah kota yang terletak di Pulau Jawa adalah benar. Pernyataan Palembang adalah kota yang terletak di Pulau Jawa adalah salah. Sehingga pernyataan Bandung atau Palembang adalah kota yang terletak di Pulau Jawa bernilai benar.

• Implikasi (⟹)

Implikasi bisa dipandang sebagai hubungan antara dua pernyataan di mana pernyataan kedua merupakan konsekuensi logis dari pernyataan pertama. Implikasi ditandai dengan notasi ‘⟹’. Misalkan p, q adalah pernyataan, implikasi berikut 

p ⟹ q

dibaca ‘jika p maka q’. Berikut adalah tabel kebenaran disjungsi.

p	q	p⇒q
B	B	B
B	S	S
S	B	B
S	S	B

Dari tabel diatas dapat disimpulkan bahwa dalam konsep implikasi akan bernilai salah jika dan hanya jika sebab bernilai benar namun akibat bernilai salah. Selain itu implikasi bernilai benar.

Contoh:

Jika Budi sembuh maka Budi akan sekolah

Jika betul Budi sembuh lalu Budi masuk sekolah, Budi telah melakukan hal yang benar. Namun jika Budi sembuh namun dia tidak masuk sekolah, Budi telah berbuat salah karena mengingkari janjinya. Lalu, bagaimana jika Budi belum sembuh? Perhatikan bahwa Budi hanya berjanji masuk sekolah jika dia sembuh. Akibatnya jika dia masih belum sembuh, tidak masalah bagi Budi untuk masuk sekolah ataupun tidak karena dia tidak melanggar janjinya.

• Biimplikasi

Suatu pernyataan p dan q dapat digabungkan dengan menggunakan kata hubung ‘jika dan hanya jika’ sehingga membentuk pernyataan majemuk ‘p jika dan hanya jika q’ yang disebut biimplikasi yang dilambangkan dengan “p ⇔ q”. Berikut adalah tabel kebenaran biimplikasi:

p	q	p⇔q
B	B	B
B	S	S
S	B	S
S	S	B

Dari tabel diatas dapat disimpulkan bahwa dalam konsep biimplikasi akan bernilai benar jika sebab dan akibatnya (pernyataan p dan q) bernilai sama. Baik itu sama-sama benar, atau sama-sama salah.

Contoh:

Ayah mendapatkan gaji jika dan hanya jika ayah bekerja

Jika ayah mendapatkan gaji maka ayah bekerja dan jika ayah telah bekerja maka ayah akan mendapat gaji. Sebalinya, jika ayah tidak mendapatkan gaji maka ayah sedang tidak bekerja dan jika ayah tidak bekerja maka ayah tidak akan mendapat gaji.

CONTOH SOAL & PEMBAHASAN: LOGIKA MATEMATIKA

Soal 1

Tentukan pernyataan P(k + 1) untuk masing-masing pernyataan P(k) berikut.

1. P(k): Sk = [k²(k + 1)²]/4
2. P(k): Sk = 1 + 5 + 9 + … + [4(k – 1) – 3] + (4k – 3)
3. P(k): k + 3 < 5k²
4. P(k): 3k ≥ 2k + 1

Pembahasan

1. Kita substitusi k + 1 ke k dalam pernyataan P(k).
   
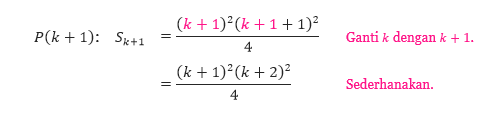
2. Untuk mendapatkan pernyataan P(k + 1), kita ganti k pada pernyataan P(k) dengan k + 1.
   
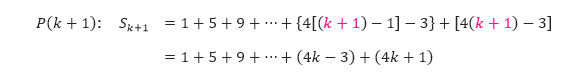
3. Kita substitusi k dengan k + 1, dan kita peroleh
   
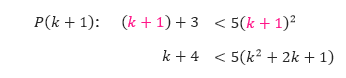
4. Serupa dengan soal-soal sebelumnya, kita substitusi k pada pernyataan P(k) dengan k + 1 untuk mendapatkan pernyataan P(k + 1).
   

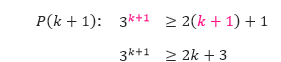
Ketika menggunakan induksi matematika untuk membuktikan rumus penjumlahan (seperti pada Soal 2), akan sangat membantu jika kita berpikir bahwa Sk + 1 = Sk + ak + 1, di mana ak + 1 adalah suku ke-(k + 1) dari penjumlahan tersebut.

Soal 2

Gunakan induksi matematika untuk membuktikan rumus

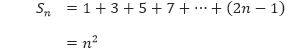
untuk semua bilangan bulat n ≥ 1.

Pembahasan Induksi matematika terdiri dari dua bagian yang berbeda.

1. Pertama, kita harus menunjukkan bahwa rumus tersebut benar ketika n = 1. Ketika n = 1, rumus tersebut benar, karena
   
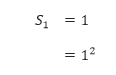
2. Bagian kedua induksi matematika memiliki dua langkah. Langkah pertama adalah menganggap bahwa rumus tersebut benar untuk sebarang bilangan bulat k. Langkah kedua adalah menggunakan anggapan ini untuk membuktikan bahwa rumus tersebut benar untuk bilangan bulat selanjutnya, k + 1. Anggap bahwa rumus
   
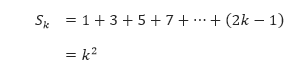
   bernilai benar, kita harus menunjukkan bahwa rumus Sk + 1 = (k + 1)² benar.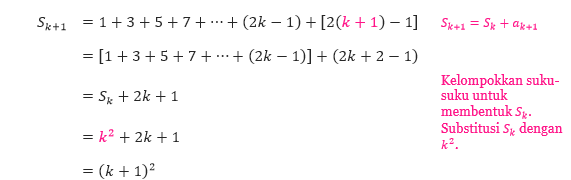
   

Dengan menggabungkan hasil pada langkah (1) dan (2), kita dapat menyimpulkan dengan induksi matematika bahwa rumus tersebut benar untuk semua bilangan bulat n ≥ 1.

Soal 3

Buktikan bahwa untuk setiap bilangan bulat positif n,

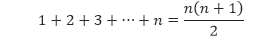
Pembahasan Misalkan P(n) adalah pernyataan 1 + 2 + 3 + … + n = n(n + 1)/2. Kita akan menunjukkan bahwa P(n) bernilai benar untuk semua bilangan bulat positif n.

1. Kita harus menunjukkan bahwa P(1) benar. Dari rumus di atas, pernyataan P(1) menyatakan
   
   dan pernyataan ini dengan jelas bernilai benar.
2. Anggap bahwa P(k) benar. Sehingga hipotesis induksi kita adalah
   
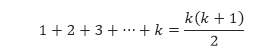
   Kita akan gunakan hipotesis tersebut untuk menunjukkan bahwa P(k + 1) benar, yaitu
   
   Sehingga, kita mulai dengan ruas kiri dan menggunakan hipotesis induksi untuk memperoleh bentuk pada ruas kanan.
   
   Sehingga kebenaran P(k + 1) mengikuti kebenaran P(k), dan kita telah melakukan langkah induksi.

Setelah membuktikan Langkah 1 dan 2, kita dapat menyimpulkan dengan Prinsip Induksi Matematika bahwa P(n) benar untuk semua bilangan bulat positif n.

---

Rangkuman berikut ini memberikan rumus-rumus untuk jumlah pangkat dari n bilangan bulat positif pertama. Rumus-rumus ini sangat penting dalam kalkulus. Rumus 1 telah kita buktikan dalam Contoh 2. Rumus-rumus yang lain juga dapat dibuktikan dengan mengunakan induksi matematika.

Soal 4

Buktikan bahwa

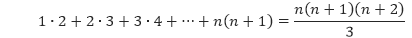
untuk semua bilangan bulat positif n.

Pembahasan Misalkan P(n) adalah pernyataan 1 ∙ 2 + 2 ∙ 3 + 3 ∙ 4 + … + n(n + 1) = [n(n + 1)(n + 2)]/3.

1. Kita akan tunjukkan bahwa P(1) bernilai benar. Berdasarkan rumus di atas, P(1) menyatakan
   
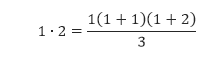
   yang bernilai benar.
2. Anggap bahwa P(k) benar dan kita memperoleh hipotesis induksi sebagai berikut.
   
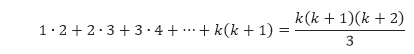
   Hipotesis ini akan kita gunakan untuk membuktikan bahwa P(k + 1) benar. Pernyataan P(k + 1) menyatakan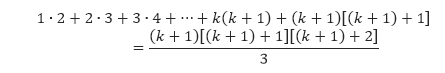
   
   Kita mulai dari bentuk yang berada di ruas kiri, kemudian kita gunakan hipotesis induksi untuk mendapatkan bentuk pada ruas kanan.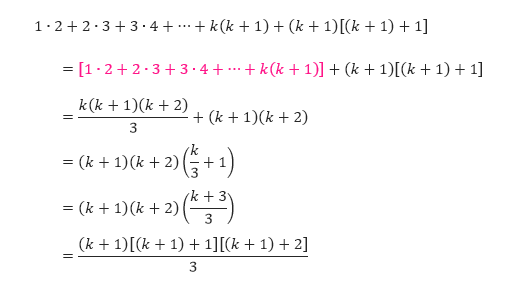
   
   Sehingga kita telah menunjukkan bahwa P(k + 1) mengikuti P(k). Sehingga kita telah membuktikan langkah induksi.

Berdasarkan Langkah 1 dan 2, kita dapat menyimpulkan dengan menggunakan induksi matematika bahwa P(n) benar untuk semua bilangan bulat positif n.

Soal 5

Buktikan bahwa

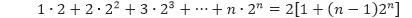
untuk semua bilangan bulat positif n.

Pembahasan Misalkan P(n) adalah pernyataan 1 ∙ 2 + 2 ∙ 2² + 3 ∙ 23 + … + n ∙ 2n = 2[1 + (n – 1)2n]

1. Pertama kita buktikan bahwa P(1) benar. Pernyataan ini menyatakan
   
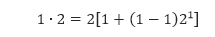
   yang dengan jelas bernilai benar.
2. Selanjutnya, kita anggap bahwa P(k) bernilai benar dan menghasilkan hipotesis induksi sebagai berikut.
   
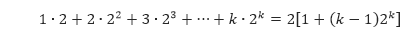
   Hipotesis induksi tersebut akan kita gunakan untuk membuktikan kebenaran P(k + 1). Pernyataan P(k + 1) mengatakan
   
   Kita mulai dari ruas kiri, kemudian kita gunakan hipotesis induksi untuk mendapatkan bentuk yang berada di ruas kanan.
   
   Sehingga pada Langkah 2 ini kita telah membuktikan bahwa jika P(k) benar maka P(k + 1) juga benar.

Jadi, berdasarkan Langkah 1 dan 2, dengan menggunakan induksi matematika kita dapat menyimpulkan bahwa P(n) bernilai benar untuk semua bilangan bulat positif n.

Soal 6

Buktikan bahwa 4n < 2n untuk semua bilangan bulat positif n ≥ 5.

Pembahasan Misalkan P(n) menyatakan pernyataan 4n < 2n.

1. P(5) adalah pernyataan 4 ∙ 5 < 25, atau 20 < 32, yang bernilai benar.
2. Anggap P(k) benar. Sehingga hipotesis induksi kita adalah
   
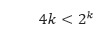
   Kita akan menggunakan hipotesis ini untuk menunjukkan bahwa P(k + 1) benar, yaitu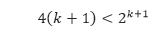
   
   Sehingga kita mulai dengan bentuk di ruas kiri pertidaksamaan tersebut dan menggunakan hipotesis induksi untuk menunjukkan bahwa bentuk tersebut kurang dari bentuk yang berada di ruas kanan. Untuk k ≥ 5 kita mendapatkan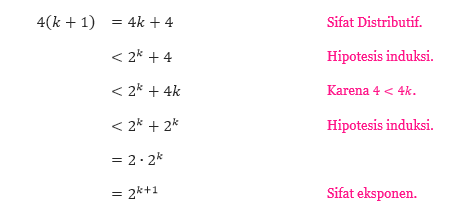
   
   Sehingga P(k + 1) mengikuti P(k), sehingga kita telah melakukan langkah induksi.

Setelah kita membuktikan Langkah 1 dan 2, kita dapat menyimpulkan dengan menggunakan Prinsip Induksi Matematika bahwa P(n) benar untuk semua bilangan bulat positif n ≥ 5.

Soal 7

Buktikan bahwa

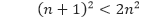
untuk semua bilangan bulat positif n ≥ 3.

Pembahasan Misalkan P(n) menyatakan (n + 1)² < 2n².

1. Pernyataan P(3), yaitu
   
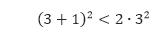
   dengan jelas bernilai benar.
2. Anggap P(k): (k + 1)² < 2k² bernilai benar, kita harus menunjukkan bahwa P(k + 1) juga bernilai benar, yaitu [(k+1) + 1]² < 2(k + 1)². Untuk k ≥3, kita memperoleh
   
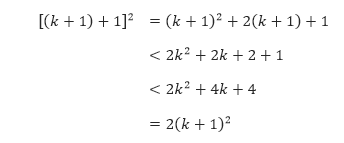
   Sehingga kita telah menunjukkan kebenaran pernyataan jika P(k) benar maka P(k + 1). Oleh karena itu, berdasarkan Langkah 1 dan 2, dengan induksi matematika kita dapat menyimpulkan bahwa P(n) benar untuk semua bilangan bulat positif n ≥ 3.

Soal 8

Buktikan bahwa n! > 2n untuk semua bilangan bulat positif n ≥ 4.

Pembahasan Misalkan P(n) merupakan notasi untuk pernyataan n! > 2n.

1. Pertama kita harus menunjukkan bahwa P(4) benar. Padahal P(4) menyatakan bahwa
   
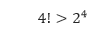
   Karena 4! = 4 ∙ 3 ∙ 2 ∙ 1 = 24 dan 24 = 16, maka P(4) benar.
2. Kita anggap bahwa P(k): k! > 2k benar. Kita akan tunjukkan P(k + 1): (k + 1)! > 2k + 1 juga bernilai benar.
   
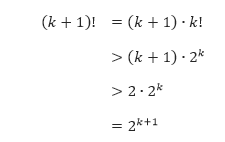
   Sehingga pada langkah induksi ini kita dapat melihat bahwa kebenaran P(k) mengakibatkan P(k + 1). Jadi, dari Langkah 1 dan 2, kita dapat menyimpulkan dengan induksi matematika bahwa P(n) bernilai benar untuk n ≥ 4.

Soal 9

Buktikan bahwa

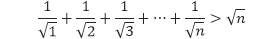
untuk semua bilangan bulat positif n ≥ 2.

Pembahasan Misalkan P(n) merupakan notasi dari pernyataan 1/√1 + 1/√2 + 1/√3 + … + 1/√n > √n.

1. Kita tunjukkan bahwa P(2) benar, yaitu
   
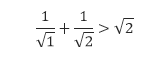
   Karena 1/√1 + 1/√2 ≈ 1,707 dan √2 ≈ 1,414 maka P(2) bernilai benar.
2. Anggap bahwa P(k) benar maka kita memperoleh hipotesis induksi seperti berikut.
   
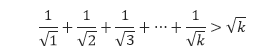
   Selanjutnya, kita tunjukkan bahwa P(k + 1) juga bernilai benar dengan menggunakan hipotesis tersebut. P(k + 1) menyatakan bahwa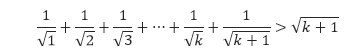
   
   Dengan menggunakan hipotesis induksi, kita ubah bentuk ruas kiri di atas menjadi bentuk yang ada di ruas kanan. Untuk k ≥ 2,
   
   Sehingga kita telah menunjukkan bahwa jika P(k) benar maka P(k + 1) benar. Jadi dengan menggunakan Prinsip Induksi Matematika kita dapat menyimpulkan bahwa P(n) benar untuk semua bilangan bulat n ≥ 2.

Soal 10

Buktikan bahwa 3 adalah faktor 4n – 1 untuk semua bilangan bulat positif n.

Pembahasan

1. Untuk n = 1, pernyataan tersebut benar karena
   
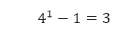
   Sehingga, 3 adalah faktor bentuk di atas.
2. Anggap bahwa 3 adalah faktor dari 4k – 1, kita harus menunjukkan bahwa 3 adalah faktor dari 4k + 1 – 1. Untuk melakukan hal ini, kita tulis seperti berikut.
   
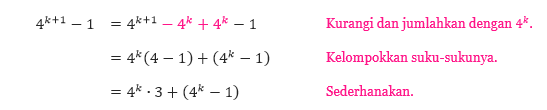
   Karena 3 adalah faktor dari 4k ∙ 3 dan 3 juga merupakan faktor 4k – 1, maka 3 adalah faktor dari 4k + 1 – 1. Dengan menggabungkan hasil pada Langkah 1 dan 2, kita dapat menyimpulkan dengan induksi matematika bahwa 3 adalah faktor 4n – 1 untuk semua bilangan bulat positif n.