1. Pengalaman matematika semester 2
2. Soal dan Pembahasan Trigonometri
Tugas Matematika
Assalamualaikum wr.wb.
Perkenalkan saya Hana Fahira, absen 15 dari X IPS 2.
Pada blog ini saya akan menceritakan pengalaman pembelajaran matematika saya selama semester ini (semester 2).
Selama semester 2 ini materi matematika yang paling saya ingat dan suka dari materi lainnya adalah tentang bab Trigonometri karena rumusnya yang walaupun mirip-mirip tapi mudah dihafal, juga konsepnya yang dapat diingat dan dipahami bila kita memang niat untuk belajar.
Sebagai murid kita dibiasakan atau menjadi terbiasa dengan mindset bahwa matematika itu tidak mudah, matematika itu sulit dan sebagainya. Hal seperti itulah yang menurut saya membuat kita (para murid) yang menjadi skeptis dan pesimis sebelum benar-benar mencoba untuk memahami dan berlatih persoalan matematika.
Oleh karena itu marilah kita mencoba merubah mindset diri masing-masing untuk menjadi lebih terbuka dengan hal baru, seperti materi atau persoalan matematika dan berlatih agar kita memiliki kepribadian yang optimis.
Begitulah pengalaman saya mengenai matematika di semester 2 sejauh ini. Untuk kedepannya semoga saya dapat lebih memahami dan semakin semangat dalam belajar matematika lagi.
Terimakasih
Nama : Hana Fahira
Kelas : X IPS 2
Absen : 15
5 Mei 2020
SOAL DAN PEMBAHASAN TRIGONOMETRI
3.7 Menyelesaikan cara merubah satuan pengukuran sudut trigonometri radian ke derajat,derajat ke radian
Konversi derajat ke radian x
rad=x⋅180∘πxrad=x⋅180∘π
Contoh 1
Ubahlah sudut-sudut berikut dalam derajat
a. π3π3 rad = ... °
b. 4π rad = ... °
Jawab :
a. π3π3 rad = π3π3 . 180∘π180∘π = 60°
b. 4π rad = 4π . 180∘π180∘π = 720°
Konversi Derajat ke Radian
x∘=x⋅π180radx∘=x⋅π180rad
Contoh 2
Ubahlah sudut-sudut berikut dalam radian
a. 30° = ... rad
b. 270° = ... rad
Jawab :
a. 30° = 30 . π180π180 rad = π6π6 rad
b. 270° = 270 . π180π180 rad = 3π23π2 rad
3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku dan sudut istimewa (600 , 300 , 450 )
Soal 1
Besar sudut yang sesuai dengan gambar di bawah adalah ⋯⋅⋯⋅
Sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni −30∘−30∘.
Karena satu putaran sama dengan 360∘360∘, maka −30∘−30∘ sama dengan (360−30)∘=330∘(360−30)∘=330∘
Jadi,besarsudutnya adalah 330∘330∘
Soal 2
Perhatikan gambar di bawah ini.
Segitiga ABCABC siku-siku di CC. Pernyataan berikut ini benar, kecuali ⋯⋅⋯⋅
A. sinα=BCABsinα=BCAB D. cosβ=BCACcosβ=BCAC
B. sinβ=ACABsinβ=ACAB E. tanα=BCACtanα=BCAC
C. cosα=ACAB
Segitiga ABCABC siku-siku di CC. Pernyataan berikut ini benar, kecuali ⋯⋅⋯⋅
A. sinα=BCABsinα=BCAB D. cosβ=BCACcosβ=BCAC
B. sinβ=ACABsinβ=ACAB E. tanα=BCACtanα=BCAC
C. cosα=ACAB
Berdasarkan gambar di atas, perbandingan trigonometri untuk sinus, cosinus, dan tangen dari sudut αα dan ββ adalah sebagai berikut.
sinα=demi=BCABcosα=sami=ACABtanα=desa=BCACsinβ=demi=ACABcosβ=sami=BCABtanβ=desa=ACBCsinα=demi=BCABcosα=sami=ACABtanα=desa=BCACsinβ=demi=ACABcosβ=sami=BCABtanβ=desa=ACBC
Jadi, dari kelima pernyataan (pilihan) yang diberikan, pernyataan yang salah ada pada pilihan jawaban D.
Soal Nomor 3
Perhatikan gambar berikut!
Nilai cosαcosα adalah ⋯⋅⋯⋅
Perhatikan gambar berikut!
Nilai cosαcosα adalah ⋯⋅⋯⋅
Dengan Teorema Pythagoras, panjang c=ABc=AB dapat ditentukan sebagai berikut.
c=√a2+b2=√(√3)2+12=√4=2c=a2+b2=(3)2+12=4=2
Cosinus sudut adalah perbandingan antara panjang sisi samping sudut terhadap hipotenusa (sisi miring) segitiga siku-siku.
Untuk itu,
cosα=bc=12cosα=bc=12
c=√a2+b2=√(√3)2+12=√4=2c=a2+b2=(3)2+12=4=2
Cosinus sudut adalah perbandingan antara panjang sisi samping sudut terhadap hipotenusa (sisi miring) segitiga siku-siku.
Untuk itu,
cosα=bc=12cosα=bc=12
3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut di berbagai kuadran
Contoh Soal 1
Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 20°
tan 40°
cos 53°
Jawab :
sin 20° = sin (90° − 70°)
= cos 70°
tan 40° = tan (90° − 50°)
= cot 50
cos 53° = cos (90° − 37°)
= sin 37°
Jika diperhatikan pada sin yang berubah menjadi cos, kemudian tan berubah jadi cot sedangkan cos berubah menjadi sin karena relasi yang dipaka adalah (90° − α) dan ketiga perbandingan trigonometri bernilai positif, karena sudut 20°, 40° dan 53° berada di kuadran I.
Contoh Soal 2
Nyatakan tiap perbandingan trigonometri berikut di dalam sudut 37° !
tan 143°
sin 233°
cos 323°
Jawab :
Sudut 143° adapada kuadran II, hingga tan 143° memiliki nilai negatif.
tan 143° = tan (180° − 37°)
= -tan 37°
Sudut 233° ada pada kuadran III, sehingga sinus memiliki nilai negatif.
sin 233° = sin (270° − 37°)
= -cos 37°
Perhatikan sin berubah menjadi cos dikarenakan relasi yang dipakai (270° − α)
Sudut 323° ada pada kuadran IV, hingga cosinus memiliki nilai positif.
cos 323° = cos (360° − 37°)
= cos 37°
3.8 Menyelesaikan soal cerita perbandingan trigonometri
Soal Nomor 1
Seorang siswa akan mengukur tinggi pohon yang berjarak 4√343 m dari dirinya. Antara mata dengan puncak pohon tersebut terbentuk sudut elevasi 30∘30∘. Jika tinggi siswa tersebut terukur sampai mata adalah 1,61,6 m, berapakah tinggi pohon?
Seorang siswa akan mengukur tinggi pohon yang berjarak 4√343 m dari dirinya. Antara mata dengan puncak pohon tersebut terbentuk sudut elevasi 30∘30∘. Jika tinggi siswa tersebut terukur sampai mata adalah 1,61,6 m, berapakah tinggi pohon?
erhatikan sketsa gambar berikut.
Misalkan xx adalah tinggi pohon terhitung dari titik yang setara dengan mata siswa itu.
Dengan menggunakan konsep tangen, diperoleh
tan30∘=x4√3x=4√3×tan30∘=4√3×13√3=43×3=4 mtan30∘=x43x=43×tan30∘=43×133=43×3=4 m
Tinggi pohon (tt) didapat dari jumlah xx dengan tinggi siswa (yang terhitung sampai mata), yaitu
t=4+1,6=5,6 mt=4+1,6=5,6 m
Jadi, tinggi pohon tersebut adalah 5,6 meter5,6 meter
Misalkan xx adalah tinggi pohon terhitung dari titik yang setara dengan mata siswa itu.
Dengan menggunakan konsep tangen, diperoleh
tan30∘=x4√3x=4√3×tan30∘=4√3×13√3=43×3=4 mtan30∘=x43x=43×tan30∘=43×133=43×3=4 m
Tinggi pohon (tt) didapat dari jumlah xx dengan tinggi siswa (yang terhitung sampai mata), yaitu
t=4+1,6=5,6 mt=4+1,6=5,6 m
Jadi, tinggi pohon tersebut adalah 5,6 meter5,6 meter
Soal Nomor 2
Seorang anak diminta untuk mengukur tinggi tiang listrik yang ada di depan sekolahnya dengan menggunakan klinometer. Pada posisi berdiri pertama dengan melihat ujung atas tiang listrik, terlihat klinometer menunjuk sudut 30∘30∘. Kemudian dia bergerak mendekati tiang listrik sejauh 1818 m dan terlihat klinometer menunjuk sudut 45∘45∘. Tinggi tiang listrik tersebut adalah ⋯⋅⋯⋅ m.
Seorang anak diminta untuk mengukur tinggi tiang listrik yang ada di depan sekolahnya dengan menggunakan klinometer. Pada posisi berdiri pertama dengan melihat ujung atas tiang listrik, terlihat klinometer menunjuk sudut 30∘30∘. Kemudian dia bergerak mendekati tiang listrik sejauh 1818 m dan terlihat klinometer menunjuk sudut 45∘45∘. Tinggi tiang listrik tersebut adalah ⋯⋅⋯⋅ m.
Perhatikan sketsa gambar berikut.
Misalkan panjang AC=xAC=x dan AD=yAD=y.
Pada segitiga ADCADC, berlaku
tan45∘=ACAD1=xyx=ytan45∘=ACAD1=xyx=y
Pada segitiga ABCABC, berlaku
tan30∘=ACAB13√3=xy+1813√3=xx+1813√3(x+18)=x(1−13√3)x=6√3x=6√31−13√3=18√33−√3x=18√33−√3×3+√33+√3x=18√3(3+√3)9−3x=3√3(3+√3)x=(9√3+9) mtan30∘=ACAB133=xy+18133=xx+18133(x+18)=x(1−133)x=63x=631−133=1833−3x=1833−3×3+33+3x=183(3+3)9−3x=33(3+3)x=(93+9) m
Jadi, tinggi tiang listrik tersebut adalah (9√3+9)(93+9) meter
Misalkan panjang AC=xAC=x dan AD=yAD=y.
Pada segitiga ADCADC, berlaku
tan45∘=ACAD1=xyx=ytan45∘=ACAD1=xyx=y
Pada segitiga ABCABC, berlaku
tan30∘=ACAB13√3=xy+1813√3=xx+1813√3(x+18)=x(1−13√3)x=6√3x=6√31−13√3=18√33−√3x=18√33−√3×3+√33+√3x=18√3(3+√3)9−3x=3√3(3+√3)x=(9√3+9) mtan30∘=ACAB133=xy+18133=xx+18133(x+18)=x(1−133)x=63x=631−133=1833−3x=1833−3×3+33+3x=183(3+3)9−3x=33(3+3)x=(93+9) m
Jadi, tinggi tiang listrik tersebut adalah (9√3+9)(93+9) meter
3.9 Menyelesaikan aturan sinus diketahui 2 sudut dan 1 sisi
1. Andi sedang mengukur mainan segitiganya yang tiap sudutnya dikodekan dengan A, B, dan C, kemudian diketahui segitiga tersebut memiliki sudut A = 30º, sisi a = 6cm dan sisi b = 8cm. Hitung besar sudut B
Akan dicari besar sudut B
sin B = (b sin A)/a
sin B = 8/6 sin 30̊
sin B = 2/3
B = arc sin B
B = arc sin (2/3)
B = 41,8̊
Jadi, besar sudut B adalah 41,8̊ atau 180̊ – 41,8̊ = 138,2̊
2. Sebuah segitiga ABC memiliki panjang AC = 4 cm. Jika besar ∠ ABC = 60o dan ∠BAC = 30o, maka panjang BC = … cm.
AC/sin ∠ABC = BC/sin∠BAC
4cm/sin 60 = BC/sin30
4cm/½√3 = BC/½
BC = ½ × 4cm/½√3
BC = 4cm/√3
BC = 4/3 √3 cm
Jadi, panjang BC adalah BC4/3 √3cm.
3.9 Menyelesaikan aturan sinus diketahui 1 sudut dan 2 sisi
Contoh 1
Diketahui suatu taman di tengah kota berbentuk segitiga sembarang. Jika sudut apit sebesar 60o dan dua sisi yang mengapitnya masing-masing panjangnya 18 meter dan 16 meter, maka luas taman tersebut adalah ….
Pembahasan:
Untuk menentukan luas segitiga sembarang yang diketahui panjang dua sisi dan sudut antara kedua sisi tersebut dapat memanfaatkan fungsi sinus.
L=1/2 x 18 x 16 x sin 60
L=1/2 x 18 x 16 x ½ √3
L= 72√3m2
Contoh 2
Di sebuah museum terdapat miniatur piramida berbentuk limas segiempat beraturan. Dari data museum diketahui panjang rusuk tegak piramida 4 meter dan membentuk sudut 30o di puncaknya. Luas satu sisi tegak piramida tersebut adalah ….
Pembahasan:
Perhatikan gambar di bawah!
Jadi, luas satu sisi tegak piramida tersebut adalah
L = ½ x 4 x 4 x sin 30
L = ½ x 4 x 4 x ½
L= 4m2 = 400 dm2
3.9 Menyelesaikan Luas segitiga jika diketahui: 1 sudut 2 sisi, 3 sisi, 2 sudut 1 sisi
contoh 1
pada segitiga ABC diketahui panjang sisi b dan sisi c berturut-turut adalah 8 cm dan 10 cm jika sudut A adalah 37 derajat, maka tentukanlah luas segitiga tersebut..
pembahasan
Dik: b = 8 cm, c = 10 cm, A = 37 derajat
Dit: L = ...?
L = ½ bc sin A
L= ½ (8) (10) sin 37 derajat
L= 40(3/5)
L= 24 cm
3.10 Menyelesaikan sudut elevasi, sudut depresi
Contoh :
1). Sebuah gedung yang tingginya 50 m dan terdapat sebuah bola di dekat gedung. Jika sudut depresi dari puncak gedung terhadap bola adalah 30∘,30∘, maka tentukan jarak bola ke dasar gedung?
Penyelesaian :
*). Ilustrasi gambar gedungnya
1). Sebuah gedung yang tingginya 50 m dan terdapat sebuah bola di dekat gedung. Jika sudut depresi dari puncak gedung terhadap bola adalah 30∘,30∘, maka tentukan jarak bola ke dasar gedung?
Penyelesaian :
*). Ilustrasi gambar gedungnya
*). Menentukan jarak bola ke dasar gedung (nilai xx ).Perhatikan segitiga ABC, yang ditanyakan nilai xx yang merupakan sisi samping, dan diketahui sisi didepan sudut, sehingga kita menggunakan tan.
tan∠BACtan30∘13–√x=desa=BCBA=50x=50x=503–√tan∠BAC=desa=BCBAtan30∘=50x13=50xx=503
Jadi, jarak bola ke dasar gedung adalah 503–√503 m .
2). Perhatikan gambar dibawah ini ,
Dua orang guru dengan tinggi badan yang sama yaitu 170 cm sedang berdiri memandang puncak tiang bendera di sekolahnya. Guru pertama berdiri tepat 10 m di depan guru kedua. Jika sudut elevasi guru pertama 60∘60∘ dan guru kedua 30∘30∘ maka dapatkah anda menghitung tinggi tiang bendera tersebut?Penyelesaian :
*). Ilustrasi gambar
Misalkan panjang CD = BG = xx
*). Menentukan nilai xx
Segitiga ABG :
tan60∘=ABx→AB=xtan60∘→AB=3–√xtan60∘=ABx→AB=xtan60∘→AB=3x
Segitiga ABF , substitusi AB=3–√xAB=3x
tan30∘13–√3–√.3–√x3x2xx=ABBF=3–√xx+10=x+10=x+10=10=5tan30∘=ABBF13=3xx+103.3x=x+103x=x+102x=10x=5
*). Menentukan tinggi tiang bendera (A)
AB=3–√x=3–√.5=53–√AB=3x=3.5=53
Jadi, tinggi tiang bendera adalah 53–√53 m .
*). Menentukan nilai xx
Segitiga ABG :
tan60∘=ABx→AB=xtan60∘→AB=3–√xtan60∘=ABx→AB=xtan60∘→AB=3x
Segitiga ABF , substitusi AB=3–√xAB=3x
tan30∘13–√3–√.3–√x3x2xx=ABBF=3–√xx+10=x+10=x+10=10=5tan30∘=ABBF13=3xx+103.3x=x+103x=x+102x=10x=5
*). Menentukan tinggi tiang bendera (A)
AB=3–√x=3–√.5=53–√AB=3x=3.5=53
Jadi, tinggi tiang bendera adalah 53–√53 m .
3.10 Menyelesaikan fungsi trigonometri dengan menggunakan lingkaran satuan untuk menentukan periode maksimum dan minimum
Soal Nomor 1
Diketahui grafik fungsi y1=5sinxy1=5sinx dan y2=sin5xy2=sin5x. Pernyataan berikut yang benar adalah ⋯⋅⋯⋅
A. periode y1y1 = periode y2y2
B. amplitudo y1y1 = amplitudo y2y2
C. periode y1=15y1=15 kali periode y2y2
D. amplitudo y1=15y1=15 kali amplitudo y2y2
E. amplitudo y1=5y1=5 kali amplitudo y2
Diketahui grafik fungsi y1=5sinxy1=5sinx dan y2=sin5xy2=sin5x. Pernyataan berikut yang benar adalah ⋯⋅⋯⋅
A. periode y1y1 = periode y2y2
B. amplitudo y1y1 = amplitudo y2y2
C. periode y1=15y1=15 kali periode y2y2
D. amplitudo y1=15y1=15 kali amplitudo y2y2
E. amplitudo y1=5y1=5 kali amplitudo y2
Pembahasan
Bentuk umum fungsi sinus tersebut adalah y=asinkxy=asinkx.
Periode:
Periode y1=5sinxy1=5sinx dengan k=1k=1 adalah P1=360∘1=360∘P1=360∘1=360∘, sedangkan periode y2=sin5xy2=sin5x dengan k=5k=5 adalah P2=360∘5=72∘P2=360∘5=72∘.
Dapat disimpulkan bahwa periode y1y1 sama dengan 5 kali periode y2y2.
Amplitudo:
Amplitudo y1=5sinxy1=5sinx dengan a=5a=5 adalah A1=|a|=|5|=5A1=|a|=|5|=5, sedangkan amplitudo y2=sin5xy2=sin5x dengan a=1a=1 adalah A2=|a|=|1|=1A2=|a|=|1|=1. Dapat disimpulkan bahwa amplitudo y1y1 5 kali amplitudo y2y2.
Pernyataan yang benar ada pada pilihan E.
Soal Nomor 2
Grafik di atas adalah grafik fungsi ⋯⋅⋯⋅
Pembahasan
Perhatikan sketsa gambar berikut.
dari grafik sinus yang memiliki bentuk umum f(x)=asinkxf(x)=asinkx, kurva pada gambar tidak bergeser dan berawal dari titik (0,0)(0,0). Grafik juga menunjukkan bahwa nilai maksimum dan minimum fungsi adalah 44 dan −4−4, sehinggaa=N. Maksimum−N. Minimum2=4−(−4)2=4a=N. Maksimum−N. Minimum2=4−(−4)2=4
Pada saat nilai x=180∘x=180∘, fungsi kembali bernilai 00, lalu berulang kembali seperti sebelumnya, sehingga periodenya adalah 180∘180∘, dan akibatnya
k=360∘180∘=2k=360∘180∘=2
Jadi, rumus fungsi f(x)=4sin2xf(x)=4sin2x dengan batas interval 0∘≤x≤270∘
Soal Nomor 3
Grafik fungsi berikut adalah sketsa grafik dari y=acoskxy=acoskx. Nilai aa dan kk berturut-turut adalah ⋯⋅⋯⋅
Nilai aa ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
a=N. Maksimum−N. Minimum2=2−(−2)2=2a=N. Maksimum−N. Minimum2=2−(−2)2=2
Grafik menunjukkan bahwa saat x=0x=0, nilai fungsinya −2−2, begitu juga saat x=2πx=2π. Ini berarti, periode grafiknya adalah 2π2π, sehingga dengan menggunakan rumus periode, diperoleh
2π=2πk⇔k=12π=2πk⇔k=1
Jadi, aa dan kk berturut-turut adalah a=−2a=−2 dan k=1k=1
Dalam sebuah segitiga ABC diketahui besar sudut B dan C berturut-turut yaitu 30o dan 37o. Jika panjang sisi di antara dua sudut tersebut yaitu 8 cm, maka tentukanlah luas segitiga tersebut.
Pembahasan :
Dik : B = 30o, C = 37o, a = 8 cm
Dit : L = .... ?
Langkah pertama kita tentukan besar sudut A :
⇒ A + B + C = 180o
⇒ A = 180o - (B + C)
⇒ A = 180o - (30o + 37o)
⇒ A = 180o - 67o
⇒ A = 113o
Berdasarkan rumus di atas :
⇒ L = a2 sin B sin C
2 sin A
⇒ L = 82 sin 30o sin 37o
2 sin 113o
⇒ L = 64 (0,5) (0,6)
2 (0,92)
⇒ L = 19,2
1,84
⇒ L = 10,42 cm
Jadi, luas segitiga tersebut yaitu 10,42 cm.
---------------------------------------------------------------------------------------------------------
Dalam sebuah segitiga ABC diketahui besar sudut A dan C berturut-turut yaitu 53o dan 30o. Jika panjang sisi di hadapan sudut B yaitu 6 cm, maka tentukanlah luas segitiga tersebut.
Pembahasan :
Dik : A = 53o, C = 30o, b = 6 cm
Dit : L = .... ?
Langkah pertama kita tentukan besar sudut B :
⇒ A + B + C = 180o
⇒ B = 180o - (A + C)
⇒ B = 180o - (53o + 30o)
⇒ B = 180o - 83o
⇒ B = 97o
Berdasarkan rumus di atas :
⇒ L = b2 sin A sin C
2 sin B
⇒ L = 62 sin 53o sin 30o
2 sin 97o
⇒ L = 36 (0,8) (0,5)
2 (0,99)
⇒ L = 14,4
1,98
⇒ L = 7,27 cm2
Jadi, luas segitiga tersebut yaitu 7,27 cm2.
---------------------------------------------------------------------------------------------------------
Diketahui sebuah segitiga PQR memiliki luas sebesar 96cm2. Jika panjang PR = 12cm dan besar ∠PRQ = 60o, tentukan panjang QR!
Pembahasan :
L = ½ × PR × QR × Sin ∠PRQ
96cm2 = ½ × 12cm × QR × Sin 60o
96cm2 = ½ × 12cm × QR × ½√3
96cm2 = 4√3cm × QR
QR = 96cm2 ÷ 4√3cm
QR = 24/√3 cm
QR = 8√3cm
Jadi, panjang QR adalah 8√3cm.
-------------------------------------------------------------------------------------------------------------------------
Mengubah atau Mengkonversi Koordinat Polar ke Koordinat Kartesius. Koordinat kartesius dari titik (10, 315°) adalah…
pembahasan :
» Sudut 315° (kuadran IV) —–> (x, -y)
» Dari pilihan jawaban di atas maka kemungkinan jawabannya D atau E
» (r, α) ——> (10, 315°)
x = 10 . cos 315°
x = 10 . ½√2
x = 5√2
y = 10 . sin 315°
y = 10 . -½√2
y = -5√2
Jadi koordinat kartesiusnya adalah (5√2, -5√2)
-------------------------------------------------------------------------------------------------------
Untuk koordinat kutub ke koordinat kartesius
Jika diketahui koordinat kutub (6√3, 60°), maka koordinat kartesiusnya adalah…
pembahasan :
koordinat kutub ⇒ koordinat kartesius
(r , α) ⇒ ( x , y )
r = 6√3 ; α = 60°
(Karena α sudut di kuadran I, maka x positif f dan y positif)
x = r cos α
⇒ 6√3 x cos 60°
⇒ 6√3 x 1/2
⇒ 3√3
y = r sin α
⇒ 6√3 x sin 60°
⇒ 6√3 x 1/2 √3
⇒ 3 x 3
⇒ 9
sehingga koordinat kartesiusnya ialah ( 3√3 , 9)
a=N. Maksimum−N. Minimum2=2−(−2)2=2a=N. Maksimum−N. Minimum2=2−(−2)2=2
Grafik menunjukkan bahwa saat x=0x=0, nilai fungsinya −2−2, begitu juga saat x=2πx=2π. Ini berarti, periode grafiknya adalah 2π2π, sehingga dengan menggunakan rumus periode, diperoleh
2π=2πk⇔k=12π=2πk⇔k=1
Jadi, aa dan kk berturut-turut adalah a=−2a=−2 dan k=1k=1
Dalam sebuah segitiga ABC diketahui besar sudut B dan C berturut-turut yaitu 30o dan 37o. Jika panjang sisi di antara dua sudut tersebut yaitu 8 cm, maka tentukanlah luas segitiga tersebut.
Pembahasan :
Dik : B = 30o, C = 37o, a = 8 cm
Dit : L = .... ?
Langkah pertama kita tentukan besar sudut A :
⇒ A + B + C = 180o
⇒ A = 180o - (B + C)
⇒ A = 180o - (30o + 37o)
⇒ A = 180o - 67o
⇒ A = 113o
Berdasarkan rumus di atas :
⇒ L = a2 sin B sin C
2 sin A
⇒ L = 82 sin 30o sin 37o
2 sin 113o
⇒ L = 64 (0,5) (0,6)
2 (0,92)
⇒ L = 19,2
1,84
⇒ L = 10,42 cm
Jadi, luas segitiga tersebut yaitu 10,42 cm.
---------------------------------------------------------------------------------------------------------
Dalam sebuah segitiga ABC diketahui besar sudut A dan C berturut-turut yaitu 53o dan 30o. Jika panjang sisi di hadapan sudut B yaitu 6 cm, maka tentukanlah luas segitiga tersebut.
Pembahasan :
Dik : A = 53o, C = 30o, b = 6 cm
Dit : L = .... ?
Langkah pertama kita tentukan besar sudut B :
⇒ A + B + C = 180o
⇒ B = 180o - (A + C)
⇒ B = 180o - (53o + 30o)
⇒ B = 180o - 83o
⇒ B = 97o
Berdasarkan rumus di atas :
⇒ L = b2 sin A sin C
2 sin B
⇒ L = 62 sin 53o sin 30o
2 sin 97o
⇒ L = 36 (0,8) (0,5)
2 (0,99)
⇒ L = 14,4
1,98
⇒ L = 7,27 cm2
Jadi, luas segitiga tersebut yaitu 7,27 cm2.
---------------------------------------------------------------------------------------------------------
Diketahui sebuah segitiga PQR memiliki luas sebesar 96cm2. Jika panjang PR = 12cm dan besar ∠PRQ = 60o, tentukan panjang QR!
Pembahasan :
L = ½ × PR × QR × Sin ∠PRQ
96cm2 = ½ × 12cm × QR × Sin 60o
96cm2 = ½ × 12cm × QR × ½√3
96cm2 = 4√3cm × QR
QR = 96cm2 ÷ 4√3cm
QR = 24/√3 cm
QR = 8√3cm
Jadi, panjang QR adalah 8√3cm.
-------------------------------------------------------------------------------------------------------------------------
Mengubah atau Mengkonversi Koordinat Polar ke Koordinat Kartesius. Koordinat kartesius dari titik (10, 315°) adalah…
pembahasan :
» Sudut 315° (kuadran IV) —–> (x, -y)
» Dari pilihan jawaban di atas maka kemungkinan jawabannya D atau E
» (r, α) ——> (10, 315°)
x = 10 . cos 315°
x = 10 . ½√2
x = 5√2
y = 10 . sin 315°
y = 10 . -½√2
y = -5√2
Jadi koordinat kartesiusnya adalah (5√2, -5√2)
-------------------------------------------------------------------------------------------------------
Untuk koordinat kutub ke koordinat kartesius
Jika diketahui koordinat kutub (6√3, 60°), maka koordinat kartesiusnya adalah…
pembahasan :
koordinat kutub ⇒ koordinat kartesius
(r , α) ⇒ ( x , y )
r = 6√3 ; α = 60°
(Karena α sudut di kuadran I, maka x positif f dan y positif)
x = r cos α
⇒ 6√3 x cos 60°
⇒ 6√3 x 1/2
⇒ 3√3
y = r sin α
⇒ 6√3 x sin 60°
⇒ 6√3 x 1/2 √3
⇒ 3 x 3
⇒ 9
sehingga koordinat kartesiusnya ialah ( 3√3 , 9)
Nama : Hana Fahira
Kelas : X IPS 2
Absen : 15
SOAL DAN PEMBAHASAN TRIGONOMETRI
1. Diketahui sebuah segitiga PQR memiliki luas sebesar 96cm2. Jika panjang PR = 12cm dan besar ∠PRQ = 60o, tentukan panjang QR!
Pembahasan :
L = ½ × PR × QR × Sin ∠PRQ
96cm2 = ½ × 12cm × QR × Sin 60o
96cm2 = ½ × 12cm × QR × ½√3
96cm2 = 4√3cm × QR
QR = 96cm2 ÷ 4√3cm
QR = 24/√3 cm
QR = 8√3cm
Jadi, panjang QR adalah 8√3cm.
2. Dalam sebuah segitiga ABC diketahui besar sudut A dan C berturut-turut yaitu 53o dan 30o. Jika panjang sisi di hadapan sudut B yaitu 6 cm, maka tentukanlah luas segitiga tersebut.
Pembahasan :
Dik : A = 53o, C = 30o, b = 6 cm
Dit : L = .... ?
Langkah pertama kita tentukan besar sudut B :
⇒ A + B + C = 180o
⇒ B = 180o - (A + C)
⇒ B = 180o - (53o + 30o)
⇒ B = 180o - 83o
⇒ B = 97o
Berdasarkan rumus di atas :
⇒ L = b2 sin A sin C
2 sin B
⇒ L = 62 sin 53o sin 30o
2 sin 97o
⇒ L = 36 (0,8) (0,5)
2 (0,99)
⇒ L = 14,4
1,98
⇒ L = 7,27 cm2
Jadi, luas segitiga tersebut yaitu 7,27 cm2.
3. Dalam sebuah segitiga ABC diketahui besar sudut B dan C berturut-turut yaitu 30o dan 37o. Jika panjang sisi di antara dua sudut tersebut yaitu 8 cm, maka tentukanlah luas segitiga tersebut.
Pembahasan :
Dik : B = 30o, C = 37o, a = 8 cm
Dit : L = .... ?
Langkah pertama kita tentukan besar sudut A :
⇒ A + B + C = 180o
⇒ A = 180o - (B + C)
⇒ A = 180o - (30o + 37o)
⇒ A = 180o - 67o
⇒ A = 113o
Berdasarkan rumus di atas :
⇒ L = a2 sin B sin C
2 sin A
⇒ L = 82 sin 30o sin 37o
2 sin 113o
⇒ L = 64 (0,5) (0,6)
2 (0,92)
⇒ L = 19,2
1,84
⇒ L = 10,42 cm
Jadi, luas segitiga tersebut yaitu 10,42 cm.
4. Untuk koordinat kutub ke koordinat kartesius
Jika diketahui koordinat kutub (6√3, 60°), maka koordinat kartesiusnya adalah…
Pembahasan :
koordinat kutub ⇒ koordinat kartesius
(r , α) ⇒ ( x , y )
r = 6√3 ; α = 60°
(Karena α sudut di kuadran I, maka x positif f dan y positif)
x = r cos α
⇒ 6√3 x cos 60°
⇒ 6√3 x 1/2
⇒ 3√3
y = r sin α
⇒ 6√3 x sin 60°
⇒ 6√3 x 1/2 √3
⇒ 3 x 3
⇒ 9
sehingga koordinat kartesiusnya ialah ( 3√3 , 9)
5. Mengubah atau Mengkonversi Koordinat Polar ke Koordinat Kartesius. Koordinat kartesius dari titik (10, 315°) adalah…
Pembahasan :
» Sudut 315° (kuadran IV) —–> (x, -y)
» Dari pilihan jawaban di atas maka kemungkinan jawabannya D atau E
» (r, α) ——> (10, 315°)
x = 10 . cos 315°
x = 10 . ½√2
x = 5√2
y = 10 . sin 315°
y = 10 . -½√2
y = -5√2
Jadi koordinat kartesiusnya adalah (5√2, -5√2)
6. Diketahui segitiga abc dengan ab= 6 cm,ac= 8 cm sudut a= 150 derajat. Luas segitiga abc
Pembahasan :
L = ½.ab.ac.Sin a
L = ½.6.8.Sin 150°
L = 12 cm²
7. Nyatakan sudut 0,45 radian dan 0,89 radian ke dalam satuan derajat!
Pembahasan:
0,45 radian = 0,45 x 180°/π
0,45 radian = 25,80°
0,89 radian = 0,89 x 180°/π
0,89 radian = 51,02°
8. Budi melihat puncak menara dengan sudut elevasi 30°. Jika jarak antara Budi dan menara yang dilihatnya adalah 150 m dan tinggi Budi adalah 120 cm maka tinggi menara tersebut adalah …
Pembahasan
tan 30⁰ = \frac{x}{150}
\frac{1}{3} \sqrt{3} = \frac{x}{150}
x = \frac{1}{3} \sqrt{3} . 150
x = 50√3
Jadi tinggi menara adalah
= x + tinggi Budi
= 50√3 m + 120 cm
= 50√3 m + 1,2 m
= (50√3 + 1,2) m
9. Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 50°tan 40°
cos 35°
Pembahasan :
sin 50° = sin (90° − 400°) = cos 40°
tan 40° = tan (90° − 50°) = cot 50°
cos 35° = cos (90° − 55°) = sin 55°
Ketiganya bernilai positif, karena sudut 50°, 40° dan 35° berada di kuadran I.
10. Tentukan nilai-nilai perbandingan trigonometri pada titik berikut: B(5, 12)
Pembahasan :
*). Menentukan jarak bola ke dasar gedung (nilai xx ).
Perhatikan segitiga ABC, yang ditanyakan nilai xx yang merupakan sisi samping, dan diketahui sisi didepan sudut, sehingga kita menggunakan tan.
tan∠BACtan30∘13–√x=desa=BCBA=50x=50x=503–√tan∠BAC=desa=BCBAtan30∘=50x13=50xx=503
Jadi, jarak bola ke dasar gedung adalah 503–√503 m .
Pembahasan:
a=N. Maksimum−N. Minimum2=4−(−4)2=4a=N. Maksimum−N. Minimum2=4−(−4)2=4
Pembahasan:
B (5, 12)
r² = x² + y²
r² = 5² + 12²
r² = 25 + 144
r² = 169
r = √169
r = 13
Pembahasan:
Nilai perbandingan trigonometrinya adalah:
Nilai perbandingan trigonometrinya adalah:
Sin α = 12/13
Cos α = 5/13
Tan α = 12/5
Cosec α = 13/12
Sec α = 13/5
Cot α = 5/12
11. Nyatakan sudut-sudut berikut dalam satuan radian (rad):
a) 270°
b) 330°
Pembahasan:
Konversi:
1 π radian = 180°
Jadi:
a) 270°
= 270° x r/180°
= 3/2 r rad
b) 330°
= 330° x r/180°
= 11/6 r rad
12. Tentukan nilai dari sec 330° . tan 120° . sin 315°
Jawaban :
Kuadran 1 : nilai trigonometrinya positif semua
Kuadran 2 : hanya nilai sin α dan cosec α yang bernilai positif
=> (180° - α)
Kuadran 3 : hanya nilai tan α dan cot α yang bernilai positif
=> (180° + α)
Kuadran 4 : hanya nilai cos α dan sec α yang bernilai positif
=> (360° - α)
sec 330°
= sec (360° - 30°)
= sec 30°
= 1/(cos 30°)
= 1/(1/2 √3)
= 2/√3
= 2/√3 . √3/√3
= (2/3) √3
tan 120°
= tan (180° - 60°)
= - tan 60°
= - √3
sin 315°
= sin (360° - 45°)
= - sin 45°
= (-1/2) √2
sec 330° . tan 120° . sin 315°
= (2/3) √3 . - √3 . (-1/2) √2
= (2/3) . 3 . (1/2) √2
= 2 . (1/2) √2
= √2
Jadi, Nilai dari sec 330° . tan 120° . sin 315° ialah √2
13. Jika sin x = 4/5 dan 90<x<180 maka tan x° =....
Jawaban :
Nilai Fungsi
90 < x < 180 , x di kuadran ke II
sin x = 4/5
cos x = √(1 - sin² x) = √(1 - (4/5)²) = √(9/25) = +- 3/5
cos x di KD II, nilai negatif
cos x = - 3/5
tan x = sin x / cos x = (4/5)/(-3/5) = - 4/3
14. Diketahui perbandingan sisi-sisi segitiga ABC adalah 2:3:4. Nilai kosinus sudut terbesar adalah....
Pembahasan :
Sisi ABC , AB = 2x , BC = 3x , AC = 4x
Sudut terbesar didepan sisi terpanjang ,
sisi terpanjang = AC
sudut terbesar = < B
cos B = (AB² + BC² - AC²) / (2)(AB)(BC)
cos B = (2x)²+(3x)² -(4x)² / 2(2x)(3x)
cos B = (4+9 -16) x²/ (12) x²
cos B = (-3)/(12)
cos B = - 1/4
15. Dalam sebuah segitiga ABC diketahui besar sudut A dan C berturut-turut yaitu 53o dan 30o. Jika panjang sisi di hadapan sudut B yaitu 6 cm, maka tentukanlah luas segitiga tersebut.
Pembahasan :
Langkah pertama kita tentukan besar sudut B :
⇒ A + B + C = 180o
⇒ B = 180o - (A + C)
⇒ B = 180o - (53o + 30o)
⇒ B = 180o - 83o
⇒ B = 97o
Berdasarkan rumus di atas :
⇒ A + B + C = 180o
⇒ B = 180o - (A + C)
⇒ B = 180o - (53o + 30o)
⇒ B = 180o - 83o
⇒ B = 97o
Berdasarkan rumus di atas :
| ⇒ L = | b2 sin A sin C |
| 2 sin B |
| ⇒ L = | 62 sin 53o sin 30o |
| 2 sin 97o |
| ⇒ L = | 36 (0,8) (0,5) |
| 2 (0,99) |
| ⇒ L = | 14,4 |
| 1,98 |
⇒ L = 7,27 cm2
Jadi, luas segitiga tersebut yaitu 7,27 cm2.
Jadi, luas segitiga tersebut yaitu 7,27 cm2.
16. Diketahui suatu taman di tengah kota berbentuk segitiga sembarang.
Jika sudut apit sebesar 60o dan dua sisi yang mengapitnya masing-masing
panjangnya 18 meter dan 16 meter, maka luas taman tersebut adalah ….
Jika sudut apit sebesar 60o dan dua sisi yang mengapitnya masing-masing
panjangnya 18 meter dan 16 meter, maka luas taman tersebut adalah ….
Pembahasan:
Untuk menentukan luas segitiga sembarang yang diketahui panjang dua sisi dan sudut antara kedua sisi tersebut dapat memanfaatkan fungsi sinus.
![\[ L = \frac{1}{2} \times 18 \times 16 \times sin \; 60^{o} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ac01cd707d0e045a1e210520eb819cf8_l3.png "Rendered by QuickLaTeX.com")
![\[ L = \frac{1}{2} \times 18 \times 16 \times \frac{1}{2} \sqrt{3} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-63d01e5d865aa1d109a909c153fab861_l3.png "Rendered by QuickLaTeX.com")
![\[ L = 72 \sqrt{3} \; \textrm{m}^{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-89d6405345ee8d8716bde9247e1a03c0_l3.png "Rendered by QuickLaTeX.com")
Pembahasan:
Ilustrasi gambar gedungnya
Ilustrasi gambar gedungnya
*). Menentukan jarak bola ke dasar gedung (nilai xx ).
Perhatikan segitiga ABC, yang ditanyakan nilai xx yang merupakan sisi samping, dan diketahui sisi didepan sudut, sehingga kita menggunakan tan.
tan∠BACtan30∘13–√x=desa=BCBA=50x=50x=503–√tan∠BAC=desa=BCBAtan30∘=50x13=50xx=503
Jadi, jarak bola ke dasar gedung adalah 503–√503 m .
18. Grafik di atas adalah grafik fungsi ⋯⋅⋯⋅
Pembahasan:
Perhatikan sketsa gambar berikut.
dari grafik sinus yang memiliki bentuk umum f(x)=asinkxf(x)=asinkx, kurva pada gambar tidak bergeser dan berawal dari titik (0,0)(0,0). Grafik juga menunjukkan bahwa nilai maksimum dan minimum fungsi adalah 44 dan −4−4, sehinggaa=N. Maksimum−N. Minimum2=4−(−4)2=4a=N. Maksimum−N. Minimum2=4−(−4)2=4
Pada saat nilai x=180∘x=180∘, fungsi kembali bernilai 00, lalu berulang kembali seperti sebelumnya, sehingga periodenya adalah 180∘180∘, dan akibatnya
k=360∘180∘=2k=360∘180∘=2
Jadi, rumus fungsi f(x)=4sin2xf(x)=4sin2x dengan batas interval 0∘≤x≤270∘
19. Fungsi yang sesuai dengan grafik berikut adalah?
Pembahasan:
Beranjak dari grafik sinus: karena kurva bergeser (ke kiri) sejauh π2, maka bentuk umum grafik fungsinya adalah f(x)= y = a sin k(x−c).
Untuk grafik ini, nilai c yang menentukan pergeseran kurva adalah −π2 (tandanya negatif, karena grafik bergeser ke kiri).
Dimulai dari titik x =−π2 yang nilai fungsinya 0, grafik fungsi kembali bernilai 0 dan berulang kembali di titik x =3π2, sehingga periode grafik fungsinya adalah 3π2–(−π2)=2π.
Dengan demikian,
k = 2π Periode = 2π
2π =1
Nilai a ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
a=N. Maksimum−N. Minimum2=2−(−2)2=2
Jadi, rumus grafik fungsinya adalah f(x)=2sin1(x+π2)=2sin(x+π2)
Untuk grafik ini, nilai c yang menentukan pergeseran kurva adalah −π2 (tandanya negatif, karena grafik bergeser ke kiri).
Dimulai dari titik x =−π2 yang nilai fungsinya 0, grafik fungsi kembali bernilai 0 dan berulang kembali di titik x =3π2, sehingga periode grafik fungsinya adalah 3π2–(−π2)=2π.
Dengan demikian,
k = 2π Periode = 2π
2π =1
Nilai a ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
a=N. Maksimum−N. Minimum2=2−(−2)2=2
Jadi, rumus grafik fungsinya adalah f(x)=2sin1(x+π2)=2sin(x+π2)
20. sebuah kapal berlayar dari pelabuhan A Ke pelabuhan B dengan kecepatan 40 km/jam
selama 2 jam dengan arah 30°, kemudian melanjutkan perjalanan dari pelabuhan B menuju pelabuhan C dengan kecepatan 60 km/jam selama 2-5 jam dengan arah 150°. buatlah sketsa perjalanan kapal dan tentukan jarak antara pelabuhan A dan C!
selama 2 jam dengan arah 30°, kemudian melanjutkan perjalanan dari pelabuhan B menuju pelabuhan C dengan kecepatan 60 km/jam selama 2-5 jam dengan arah 150°. buatlah sketsa perjalanan kapal dan tentukan jarak antara pelabuhan A dan C!
Pembahasan:
Jarak = kecepatan x waktu
Jarak pelabuhan A ke B adalah 40 x 2 = 80 km
Jarak pelabuhan B ke C adalah 60 x 2,5 = 150 km
Besar sudut ABC adalah 30° + 30° = 60°
Gunakan aturan cosinus untuk mencari AC
AC² = AB² + BC² - [2 x AB x BC x cos ∠ABC]
AC² = 80² + 150² - [2 x 80 x 150 x cos 60°]
AC² = 28.900 - [2 x 80 x 150 x ¹/₂]
AC² = 28.900 - 12.000
AC = √ 16.900
Diperoleh jarak antara pelabuhan A dan C sejauh 130 km
SOAL DAN PEMBAHASAN RELASI DAN FUNGSI | REMED PHB
Hana Fahira (15) X IPS 2
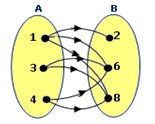
1. Relasi dari himpunan A ke himpunan B pada diagram panah di samping adalah . . .
A. kurang dari
B. setengah dari
C. lebih dari
D. faktor dari
Jawaban : A
Pembahasan :
“kurang dari” :
{(1, 2), (1, 6), (1, 8), (3, 6), (3, 8), (4, 6),(4, 8)}
2. Relasi “factor dari” dari himpunan P = {1, 2, 3} ke Q = {2, 4, 6} ditunjukkan oleh diagram panah ….
Jawaban :
Pembahasan :
” factor dari ” :
{(1, 2), (1, 4) (1, 6), (2, 2), (2, 4), (2, 6), (3, 6)}
3. K = {3, 4, 5} dan L = {1, 2, 3, 4, 5, 6, 7}, himpunan pasangan berurutan yang menyatakan relasi “dua lebihnya dari” dari himpunan K ke L adalah ….
A. {(3, 5), (4, 6)}
B. {(3, 5), (4, 6), (5, 7)}
C. {(3, 1), (4, 2), (5, 3)}
D. {(3, 2), (4, 2), (5, 2)}
Jawaban : B
Pembahasan :
” dua lebihnya dari ” dri himpunan K ke L :
3 —> 5, 4 —> 6, 5 —> 7 atau
{(3, 5), (4, 6), (5, 7)}
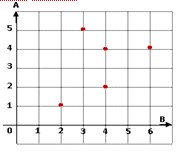
4. Himpunan pasangan berurutan dari grafik catesius di bawah adalah …
A. {(2, 1), (3, 5), (4, 4), (6, 4)}
B. {(1, 2), (2, 4), (4, 6), (5, 3)}
C. {(1, 2), (2, 4), (4, 4), (4, 6), (5, 3)}
D. {(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)}
Jawaban : D
Pembahasan :
Himpunan Pasangan berurutan dari grafik cartesius :
{(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)}
5. Range dari himpunan pasangan berurutan {(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)} adalah …
A. {1, 2, 4, 5}
B. {1, 2, 3, 4, 5}
C. {1, 2, 3, 4, 5, 6}
D. {1, 2, 3, 4, 5, 6}
Jawaban : A
Pembahasan :
Range dari {(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)}
yaitu :
{1, 2, 4, 5}
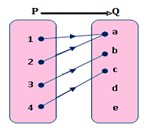
6. Diagram panah pada gambar di bawah merupakan pemetaan maka rangenya adalah. . .
A. {a, b, c}
B. {d, e}
C. {a, b, c, d, e}
D. {1, 2, 3, 4}
Jawaban : A
Pembahasan :
Rangenya adalah {a, b, c}
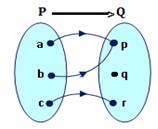
7. Daerah hasil pemetaan yang ditunjukan oleh diagram panah di bawah adalah. . .
A. {a, b, c}
B. b. {p, r}
C. {p, q, r}
D. { a, b, c, p, r}
Jawaban : B
Pembahasan :
Hasil pemetaan dari diagram panah di atas :
{p, r}
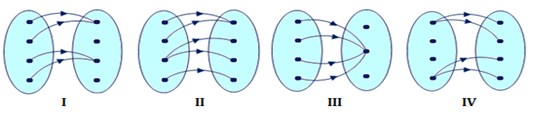
8. Dari gambar diagram panah di dibawah, yang merupakan pemetaan ialah …
A. hanya I dan II
B. hanya II dan III
C. hanyan I dan III
D. hanyan II dan IV
Jawaban : C
Pembahasan :
yang merupakan pemetaan hanya I dan III
9. Dari himpunan pasangan berurutan berikut ini :
- I. {(1, 2), (2, 2), (3, 3)}
- II. {(1, 2), (2, 2), (3, 1), (3, 2)}
- III. {(1, 1), (1, 2), (1, 3), (1, 4)}
- IV. {(1, 1), (1, 2), (2, 3), (2, 4)}
Yang merupakan pemetaan adalah …
A. IV
B. III
C. II
D. I
Jawaban : D
Pembahasan :
Yang merupakan pemetaan adalah {(1, 2), (2, 2), (3, 3)}
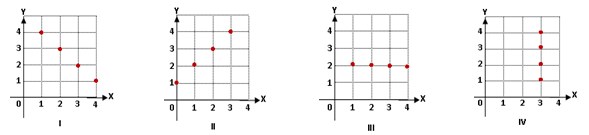
10. Dari diagram cartesius di bawah ini, yang menunjukkan pemetaan adalah ….
Dari diagram cartesius di bawah ini, yang menunjukkan pemetaan adalah ….
A. hanya I, II dan III
B. hanya I, II dan IV
C. hanya I, III dan IV
D. hanya II, III dan IV
Jawaban : A
Pembahasan :
Yang menunjukkan pemetaan hanya I, II dan III
11. Diketahui : Himpunan A = {factor dari 10} dan B = {factor prima dari 30}. Banyak semua pemetaan yang mungkin dari himpunan A ke himpunan B adalah …
A. 81
B. 64
C. 16
D. 8
Jawaban : A
Pembahasan :
A = {1, 2, 5, 10} ⇒ n(A) = 4
dn B = {2, 3, 5} ⇒ n(B) = 3
Banyak pemetaan A ⇒ B adalah 34 = 81
12. K = {factor dari 8} dan L = {bilangan prima yang kurang dari 7}. Banyak semua pemetaan yang mungkin dari himpunan K ke himpunan L adalah …
A. 100
B. 81
C. 64
D. 16
Jawaban : B
Pembahasan :
K = {1, 2, 4, 8} ⇒ n(K) = 4
L = {2, 3, 5} ⇒ n(L) = 3
n(K ⇒ L) = 34 = 81
13. Diketahui : P = {x| 11 < x <19, x bil. Prima}, Q = { y| y2< 9, y bil. Cacah}, banyak semua pemetaan yang mungkin dari himpunan P ke himpunan Q adalah …
A. 27
B. 8
C. 4
D. 2
Jawaban : C
Pembahasan :
P = {13, 17} ⇒ n(P) = 2
Q = {1, 2} ⇒ n(Q) = 2
n(P ⇒ Q) = 2² = 4
14. Banyak koresponden satu-satu yang mungkin terjadi dari himpunan P ={3, 5, 7, 9} dan Q = {p, q, r, s} adalah …
A. 4 cara
B. 8 cara
C. 16 cara
D. 24 cara
Jawaban : D
Pembahasan :
Banyaknya koresponden satu-satu :
4! = 1.2.3.4 =24 cara
15. Jika n(P) = n(Q) = 3 , maka banyaknya koresponden satu-satu antara himpunan P ke Q adalah
A. 15 cara
B. 12 cara
C. 9 cara
D. 6 cara
Jawaban : D
Pembahasan :
3! = 1.2.3 = 6 cara
16. Dari pernyataan-pernyataan berikut :
I. Siswa dengan tempat duduknya
II. Siswa dengan tanggal lahirnya
III. Negara dengan lagu kebangsaannya
Yang berkoresponden satu-satu adalah …
A. hanya II dan III
B. hanya I, II dan III
C. hanya I dan III
D. hanya I dan II
Jawaban : A
Pembahasan :
Yang berkoresponden satu-satu adalah …
- I . Siswa dengan tempat duduknya
- III. Negara dengan lagu kebangsaannya
17. Dari pernyataan berikut ini :
(i) Himpunan negara dan himpunan bendera
(ii) Semua penonton dan tiket masuk dalam pertandingan sepakbola
(iii) Semua siswa di kelasmu dan nama siswa pada daftar hadir di kelasmu
(iv) Semua siswa di sekolahmu dan guru-guru di sekolahmu
Yang berkoresponden satu-satu adalah …
A. (i), (iii), (iv)
B. (ii), (iii), (iv)
C. (i), (ii), (iii)
D. (i), (ii), (iv)
Jawaban : C
Pembahasan:
Yang berkoresponden satu-satu :
- (i) Himpunan negara dan himpunan bendera
- (ii) Semua penonton dan tiket masuk dalam pertandingan sepakbola
- (iii) Semua siswa di kelasmu dan nama siswa pada daftar hadir di kelasmu
18. Dari pasangan himpunan-himpunan berikut ini.
- (i) A = {x | 0 < x < 4, x bilangan cacah} dan B = {factor dari 4}
- (ii) P = {huruf Vokal} dan Q = {bilangan asli kurang dari 4}
- (iii) K = {a, b, c, d} dan L = {factor dari 6}
- (iv) D = {1, 2, 3, 4} dan E = {bilangan prima kurang dari 8}
Yang berkoresponden satu-satu adalah …
A. (ii), (iii), (iv)
B. (i), (ii), (iv)
C. (i), (ii), (iv)
D. (i), (iii), (iv)
Jawaban : D
Pembahasan :
Yang berkoresponden satu-satu :
- (i) A = {x | 0 < x < 4, x bilangan cacah} dan B = {factor dari 4}
- (iii) K = {a, b, c, d} dan L = {factor dari 6}
- (iv) D = {1, 2, 3, 4} dan E = {bilangan prima kurang dari 8}
19. Dari himpunan-himpunan berikut :
- A = {x| x < 4, x bilangan Asli}
- B = {x| x < 4, x bilangan Prima}
- C = {x| x < 4, x factor prima dari 70}
- D = {x| 2 < x < 10, x bilangan ganjil}
Yang berkoresponden satu-satu adalah …
A. A dan B
B. A dan C
C. B dan D
D. C dan D
Jawaban : B
Pembahasan :
Yang berkoresponden satu-satu :
A = {x| x < 4, x bilangan Asli}
C = {x| x < 4, x factor prima dari 70}
20. Dari himpunan pasangan berikut :
(i) {(a, 1), (b, 2), (c, 3), (d, 3)}
(ii) {(p, 5), (q, 7), (q, 9), (r, 11)}
(iii) {(s, 3), (t, 4), (u, 5), (v, 6)}
(iv) {(s, 3), (t, 4), (u, 3), (v, 6)}
Yang berkoresponden satu-satu adalah ..
A. (i)
B. (ii)
C. (iii)
D. (iv)
Jawaban : C
Pembahasan :
Yang berkoresponden satu-satu adalah ..
(iii) {(s, 3), (t, 4), (u, 5), (v, 6)}
No comments:
Post a Comment