HANA FAHIRA (14) XI IPS 2

3.


Fungsi Linear
Pada soal diatas diselesaikan dengan fungsi linear, untuk menyelesaikan masalah dengan model matematika yang terdiri atas pertidaksamaan linear yang mempunyai banyak kemungkinan penyelesaian. dan Dari semua hasil kemungkinan satu yang memberikan hasil yang optimal.
- Model I memerlukan 1 m kain polos dan 3 m kain bergaris.
- Model II memerlukan 2 m kain polos dan 1 m kain bergaris.
- Persediaan kain polos 20 m
- persediaan kain bergaris 20 m
- Harga jual model I Rp.150.000,00
- Harga jual model II Rp.100.000,00
- Penghasilan maksimum yang dapat diperoleh = ...
(1) Kita Buat Tabel Untuk memudahkan:
Model || Polos || Garis || Harga
I || 1 || 3 || 150.000
II || 2 || 1 || 100.000
Stok || 20 || 20 || maksimum
(2) Kita buat kalimat matematika dari Tabel diatas Dengan kain polos sebagai (x) dan kain bergaris sebagai (y) :
x + 2y ≤ 20
3x + y ≤ 20
dengan :
x ≥ 0
y ≥ 0
Dan Fungsi Tujuan adalah harga jual :
150.000x + 100.000y
(3) Tentukan nilai fungsi x dan y pada grafik fungsi :
Dari x + 2y = 20 :
x = 0, y ⇒ 0 + 2y = 20
⇒ 2y = 20
⇒ y = 20/2
⇒ y = 10
Titik Koordinat ⇒ (0,10)
y = 0, x ⇒ x + 2y = 20
⇒ x + 0 = 20
⇒ x = 20
Titik Koordinat ⇒(20,0)
Dari 3x + y = 20
x = 0 , y ⇒ 3x + y = 20
⇒ 0 + y = 20
Titik Koordinat ⇒ (0,20)
y = 0, x ⇒ 3x + y = 20
⇒ 3x + 0 = 20
⇒ 3x = 20
⇒ x = 20/3
Titik Koordinat ⇒ (20/3,0)
Dari Titik - titik tersebut tarik garis lurus hingga terhubung.
Lalu kita cari titik potong dari garis tersebut, dengan metode eliminasi dan subtitusi :
Eliminasi y :
x + 2y = 20 | x 1 | x + 2y = 20
3x + y = 20 | x 2 | 6x + 2y = 40
============ -
-5x = -20
x = 20/5
x = 4
Subtitusikan nilai x pada persamaan 3x + y = 20 :
3 . 4 + y = 20
12 + y = 20
y = 20 - 12
y = 8
Koordinat titik potong garis pada (4,8)
(4) Selanjutnya Dari Titik - titik yang berpotongan kita uji dengan :
Fungsi Tujuan f(x,y) = 150.000x + 100.000y :
Ada 3 titik pada Grafik (perhatikan lampiran)
A. Titik (0,10) = 150.000 . (0) + 100.000 . (10) =
= 0 + 1.000.000 = 1.000.000
B. Titik (4,8) = 150.000 . (4) + 100.000 . (8) =
= 600.000 + 800.000 = 1.400.000
C. Titik (20/3,0) = 150.000 . (20/3) + 100.000 . (0) =
= 1.000.000 + 0 = 1.000.000
Dari Hasil Uji diatas dapat dilihat, penghasilan terbesar pada titik (4,8) yaitu sebesar Rp.1.400.000,00
Determinan matriks A dilambangkan dengan det A atau |A|. Untuk menentukan determinan matriks dapat digunakan sebagai berikut.
1. Matriks berordo 2 x 2
Jika matriks , maka
det A = |A| =
2. Matriks berordo 3 x 3
Jika matriks
, maka
determinan A dapat ditentukan dengan menggunakan aturan Sarrus:
= a₁₁ a₂₂ a₃₃ + a₁₂ a₂₃ a₃₁ + a₁₃ a₂₁ a₃₂ - a₁₃ a₂₂ a₃₁ - a₁₁ a₂₃ a₃₂ - a₁₂ a₂₁ a₃₃
Penyelesaian
diket:
ditanya:
det C...?
jawab:
- mencari transpos matrisk A
⇒
- mencari matriks C
- mencari det C
det C = (3)(3) - (-6)(8)
= 9 + 48
det C = 57
Jadi, determinan dari matriks C adalah 57.
Jika matriks A = tidak mempunyai invers, maka nilai x adalah 1. Matriks adalah kumpulan dari angka angka yang disusun dalam baris dan kolom. Operasi hitung perkalian matriks syaratnya adalah kolom matriks pertama harus sama dengan baris matriks kedua. Matriks A berordo (m × n) bisa dikalikan dengan matriks B berordo (n × p) maka hasil perkaliannya adalah matris C yang berordo (m × p). Suatu matriks memiliki invers jika determinan matriksnya tidak sama dengan nol. Rumus invers matriks adalah:
- A⁻¹ =
× Adjoin A
Misal A = , maka
- Determinan A = |A| = ad – bc
- Invers matriks A = A⁻¹ =
Pembahasan
Diketahui
A =
Matriks A tidak mempunyai invers
Ditanyakan
x = .... ?
Jawab
Suatu matriks tidak mempunyai invers jika determinan matriks tersebut sama dengan nol
Jadi
|A| = 0
(2x + 1)(5) – 3(6x – 1) = 0
10x + 5 – 18x + 3 = 0
8 – 8x = 0
8 = 8x
x =
x = 1
Garis h = bx + 3y = 12
mg = 2/a
mh = -b/3
karena g dan h saling tegak lurus, maka mg x mh = -1, maka:
2/a . –b/3 = -1
-2b/3a = -1
2b/3a = 1
3a = 2b
Sehingga a : b= 2 : 3
22.
- Agar lebih mudah dalam membuat matriks produksi, pertama kita akan membuat tabel produksi untuk masing-masing pabrik sebagai berikut.
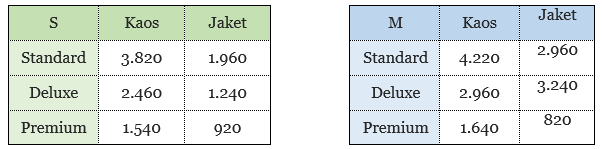
Sehingga, kita mendapatkan matriks-matriks produksi S dan M sebagai berikut.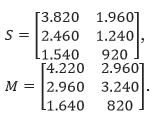
- Dari matriks yang diperoleh dari poin 1, kita dapat menghitung banyaknya pakaian yang telah diproduksi oleh pabrik di Surabaya. Banyaknya kaos yang telah diproduksi adalah 7.820, sedangkan banyaknya jaket yang sudah diproduksi adalah 4.120. Selanjutnya, banyaknya kaos yang diproduksi oleh pabrik di Malang adalah 8.820, sedangkan banyaknya jaket yang telah diproduksi adalah 7.020.
- Diketahui perkiraan peningkatan produksinya adalah 4% = 0,04. Artinya, jika n adalah banyaknya produksi pakaian tahun kemarin, maka banyaknya produksi pada tahun ini adalah n + 0,04n = 1,04n. Sehingga, matriks produksi pada tahun depan dapat ditentukan dengan menggunakan perkalian skalar sebagai berikut.
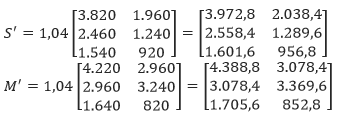
Sehingga dari matriks di atas kita mendapatkan perkiraan banyaknya pakaian yang akan diproduksi oleh JCloth di pabrik Surabaya ataupun Malang. Pabrik di Surabaya akan memproduksi kaos kurang lebih 3.973 kualitas standard, 2.558 kualitas deluxe, dan 1.602 kualitas premium serta memproduksi jaket sebanyak 2.038 kualitas standard, 1.290 kualitas deluxe, dan 956,8 kualitas premium. Sedangkan pada, pabrik di Malang akan memproduksi kaos sebanyak 4.389 kualitas standard, 3.078 kualitas deluxe, 1.706 kualitas premium serta meproduksi jaket sebanyak 3.078 kualitas standard, 3.370 kualitas deluxe, dan 852,8 kualitas premium pada periode yang sama. - Untuk menentukan banyaknya total pakaian yang diproduksi oleh JCloth, kita jumlahkan matriks S’ dengan M’ seperti berikut.

Dari penjumlahan matriks di atas, kita memperoleh informasi banyaknya pakaian yang akan diproduksi oleh JCloth. Dengan menjumlahkan semua elemen-elemen matriks penjumlahan tersebut, kita peroleh bahwa banyaknya pakaian yang akan diproduksi oleh JCloth kurang lebih 28.142.
x = pensil
5x + 3 y = 11.500 (x2)
4x + 2 y = 9.000 (x3)
_______________
10x + 6 y = 23.000
12x + 6y = 27.000
_______________ (-)
-2x = -4.000
x = 2.000
4x + 2y = 9.000
4(2000) + 2y = 9000
2y = 1000
y = 500
jadi harga pensil = 2000 dan penghapus = 500
sehingga doni harus membayar 6(2000) + 5(500) = 12.000+2.500 = 14.500
a. Nyatakan banyaknya makanan yang disetorkan setiap harinya dengan matriks
Banyaknya makanan disetorkan = A
A =
b. Nyatakan harga makanan dalam bentuk matriks
Harga makanan = B
B =
c. Hitung pemasukan Bu Ani dari setiap kantin dengan cara perkalian matriks
Perkalian Matriks A dan Matriks B
AB =
AB =
Kantin A: Rp. 55.000,00
Kantin B: Rp. 93.000,00
Kantin C: Rp. 100.000,00
d. Carilah determinan matriks dari banyaknya makanan yang disetorkan setiap harinya
|A| = (10 X 15 X 10) + (10 X 8 X 15) + (5 X 20 X 20) - (5 X 15 X 15) - (10 X 20 X 8) - (10 X 8 X 20)
|A| = -100 - 800 + 875
|A| = -15
3x + 4y = 55
Jika ditulis dalam bentuk matriks:
Jadi, Lisa bekerja selama 9 jam sedangkan Muri bekerja selama 7 jam.
Daftar Pustaka:
















No comments:
Post a Comment