HANA FAHIRA (14) XI IPS 2
PENGERTIAN MATRIKS
Matriks merupakan kumpulan pada buah bilangan yang tersusun antara baris dan kolom atau bisa disusun dengan keduannya dan kemudian dihimpit dengan tanda kurung. Matrik mempunyai elemen-elemen pada bilangan tertentu untuk penyederhanan data agar dapat dengan mudah dikelolanya.
Sebuah metrik dapat diperoleh dengan cara menukar elemen pada baris menjadi kolom atau elemen. Dan dapat disimbolkan dengan lambang tanda petik A’ atau dengan huruf T kecil diatasnya AT
JENIS-JENIS MATRIKS
Matriks Persegi
Matriks persegi merupakan matriks yang memilki banyak baris & banyak kolom yang sama. Secara umum, matriks persegi berordo n x n. Contoh dari matriks persegi seperti berikut :

Matriks Kolom
Matriks kolom merupakan matriks yang hanya satu kolom. Biasanya matriks kolom berordo m x 1. Contoh matriks kolom seperti berikut :

Matriks Baris

Matriks Transpose

Matriks Diagonal

Matriks segitiga atas & Matriks segitiga bawah

Matriks A merupakan matriks segitiga atas, sedangkan matriks B merupakan matriks segitiga bawah.
Matriks Simetri
Misalkan ada matriks A. Maka matriks A akan disebut matriks simetri apabila A’ = A atau setiap elemen-elemen pada matriks A yang letaknya simetris terhadap diagonal utama bernilai sama, yakni aij = aji dengan i tidak sama dengan j. Contoh matriks simetri, seperti berikut :

Matriks Nol
Suatu matriks akan disebut matriks nol apabila semua elemen dari matriks tersebut yakni ialah nol. Contoh matriks nol seperti berikut :

Matriks Identitas
Matriks identitas merupakan matriks diagonal yang mana seluruh elemen pada diagonal utamanya adalah 1. Matriks identitas pada umunya dinotasikan dengan I. Contoh matriks indentitas seperti berikut :

Demikianlah ulasan kami mengenai Materi makalah Pengertian Matriks dan Jenis-jenis Matriks. semoga menambah wawasan kita dan bermanfaat. Terima kasih telah berkunjung.
a. Penjumlahan dan Pengurangan Matriks
Pertama, ada operasi penjumlahan dan pengurangan matriks. Kita akan bahas satu-persatu dimulai dari operasi penjumlahannya terlebih dahulu, ya.
1. Penjumlahan matriks
Misalkan terdapat dua buah matriks, yaitu matriks A dan matriks B. Jika matriks C adalah matriks penjumlahan dari A dengan B, maka matriks C dapat diperoleh dengan menjumlahkan setiap elemen pada matriks A yang seletak dengan setiap elemen pada matriks B. Oleh karena itu, syarat agar dua atau lebih matriks dapat dijumlahkan adalah harus memiliki ordo yang sama.
Sifat-Sifat Penjumlahan Matriks:

Hasil dari A + B dapat diperoleh dengan menjumlahkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.
 Paham, ya. Selanjutnya ada operasi pengurangan matriks. Tapi, sebelum masuk ke bahasan tentang operasi pengurangan matriks, kamu harus tahu dulu istilah tentang lawan suatu matriks.
Paham, ya. Selanjutnya ada operasi pengurangan matriks. Tapi, sebelum masuk ke bahasan tentang operasi pengurangan matriks, kamu harus tahu dulu istilah tentang lawan suatu matriks.
Namanya juga lawan. Pasti antara matriks yang satu dengan matriks yang lain akan saling bertentangan. Gampangnya sih, kalau yang satu nilainya positif, pasti yang satu lagi nilainya bakal negatif. Jadi, kalau ada matriks A, maka lawan matriks A adalah suatu matriks yang elemen-elemennya merupakan lawan dari elemen-elemen matriks A tersebut.
A = [aij], lawan matriks A ditulis -A = [-aij]
2. Pengurangan matriks
Misalkan terdapat dua buah matriks, yaitu matriks A dan matriks B. Jika matriks C adalah matriks pengurangan dari A dengan B, maka matriks C dapat diperoleh dengan mengurangkan setiap elemen pada matriks A yang seletak dengan setiap elemen pada matriks B.
Pada dasarnya, pengurangan sama halnya dengan penjumlahan terhadap lawan bilangan penambah, sehingga pengurangan matriks A dengan matriks B dapat diartikan sebagai penjumlahan matriks A dengan lawan matriks B.
A - B = A + (-B)
Sama halnya dengan syarat penjumlahan matriks, dua atau lebih matriks hanya dapat dikurangkan apabila memiliki ordo yang sama, teman-teman. Nah, supaya kamu nggak bingung, kita coba kerjakan contoh soal di bawah ini, yuk.
Contoh:

Hasil dari A - B dapat diperoleh dengan mengurangkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.

Gimana? Paham ya sampai di sini. Kalau gitu, kita lanjut ke operasi aljabar matriks berikutnya, ya!
b. Perkalian Matriks
Operasi perkalian matriks dibagi menjadi dua nih, yaitu perkalian matriks dengan bilangan real (skalar) dan perkalian antarmatriks. Kita simak pembahasan berikut untuk tahu bagaimana cara menyelesaikannya, ya.
1. Perkalian matriks dengan bilangan real (skalar)
Misalkan terdapat matriks A berordo m × n dan suatu bilangan real (skalar), yaitu k. Perkalian antara matriks A dengan skalar k dapat ditulis dengan kA yang diperoleh dengan mengalikan setiap elemen matriks A dengan skalar k.

Perkalian suatu matriks dengan skalar dapat dilakukan tanpa syarat tertentu. Artinya, semua matriks dengan ordo sembarang dapat dikalikan dengan bilangan real (skalar).
2. Perkalian matriks dengan matriks
Misalkan terdapat dua buah matriks, yaitu matriks A dengan ordo m × p dan matriks B dengan ordo p × n. Perkalian matriks A dengan matriks B dapat ditulis dengan A × B yang diperoleh dari penjumlahan hasil kali elemen-elemen yang bersesuaian pada baris ke-i matriks A dengan kolom ke-j matriks B, dengan i = 1, 2, 3, ..., m dan j = 1, 2, 3, ..., n.
Syarat agar dua buah matriks dapat dikalikan adalah matriks pertama harus memiliki jumlah kolom yang sama dengan jumlah baris pada matriks kedua. Ordo matriks hasil perkalian dua buah matriks adalah jumlah baris pertama dikali jumlah kolom ke dua.
Hmm... Pasti kamu bingung ya maksudnya gimana. Oke, supaya kamu nggak bingung, kita coba kerjakan soal di bawah ini, yuks!
Contoh:

Jumlah kolom matriks A adalah 2 dan jumlah baris matriks B adalah 2. Matriks A memiliki jumlah kolom yang sama dengan jumlah baris matriks B, sehingga syarat perkalian antarmatriks sudah terpenuhi.
Selanjutnya, kita dapat mengalikan setiap elemen baris di matriks A dengan setiap elemen kolom di matriks B. Coba kamu perhatikan lingkaran berwarna pada tiap-tiap elemen matriks di bawah ini, ya. Lingkaran merah dipasangkan dengan lingkaran merah dan lingkaran biru dipasangankan dengan lingkaran biru.
Jadi, a11 akan dikalikan dengan b11, a12 dikalikan dengan b21, a21 dikalikan dengan b11, dan a22 dikalikan dengan b21.

Lalu, jumlahkan hasil kali elemen-elemennya menjadi seperti ini:

Sehingga, hasil kali matriks A dengan matriks B adalah sebagai berikut:

Sifat-Sifat Perkalian Matriks
CONTOH SOAL
Contoh Soal 1
Jika diketahui persamaan metrik !

A. 4
B. 5
C. 7
D. 29
E. 31
Pembahasannya :


Karena kedua matriks sama, maka elemen-elemen yang seletak akan sama pula, sehingga berlaku:
2x + 1 = 3
2x = 2
x = 1
y + 12 = 15
y = 3
x + y = 1 + 3 = 4
Jawabannya: A
Contoh Soal 2

Contoh Soal 3

Contoh Soal 4

Contoh Soal 5

Contoh Soal 6

Contoh Soal 7
Jika determinan nilai matriks A adalah 4 kali determinan nilai matriks B, maka nilai x adalah…
A. 4/3
B. 8/3
C. 10/4
D. 5/3
E. 16/7
Pembahasannya:
det A = 4 det B
4 x (16 x ) – (-16) = 4 (108 – (-152))
4 x (4 2x ) + 16 = 4 (260)
4 3x = 4 (260) – 16
4 3x = 4 (260) – 4 (4)
4 3x = 4 (260 – 4)
4 3x = 4 (256)
4 3x = 4. 4 4
4 3x = 4 5
3x = 5
x = 5/3
Jawabannya : D
Contoh Soal 8

Contoh Soal 9

Contoh Soal 10

A.60 derajat
B.40 derajat
C.30 derajat
D.10 derajat
E.70 derajat
Pembahasannya :
Jumlah dan selisih kedua vektor masing-masing adalah:


Jawabannya : A
Contoh Soal 11
Jika diketahui matrik a, b ,c, dari persamaan dibawah ini:
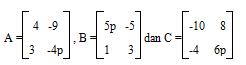
Bila persamaan A – B = C-1 , maka tentukan nilai dari 2p adalah …
A. -1
B. -1/2
C. 1/2
D. 1
E. 2
Pembahasannya :
Jika menggunakan sebuah rumus matriks ordo 2×2 sebagai berikut :


Jawabannya: D
Contoh Soal 12
Jika diketahui persamaan matrik a, b, dan c sebagai berkiut :
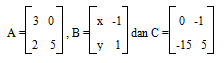
Bila At ialah gambaran dari rumusan matriks A dan At . B = C, maka tentukan nilai dari 2x + y = ….
A. -4
B. -1
C. 1
D. 5
E. 7
Pembahasannya:
Jika didapat rumusan matriks ordo 2×2 maka :
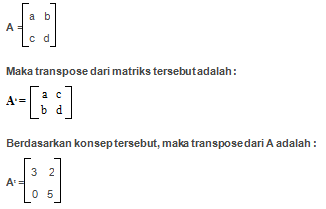

Jawabannya: C
Contoh Soal 13
Diketahui persamaan matrik A, B, dan C :
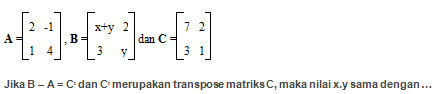
A. 10
B. 15
C. 20
D. 25
E. 30


Jawabannya: C
Contoh Soal 14
Diketahui A = 


- A + B :
- A + C :
Penyelesaian :
- A + B =


- A + C =

Contoh Soal 15
Jika A = 

Penyelesaian :
- B – A =


- B – A =


Sifat dari penjumlahan dan pengurangan sebuah matriks yaitu :
- A + B = B + A
- (A + B) + C = A + (B + C)
- A – B ≠ B – A
Contoh Soal 16
Jika matriks 

Pembahasannya :
Diketahui bahwa kedua matriks diatas tersebut saling invers, maka berlaku syarat AA-1 = A-1A = I.
Maka :


Sehingga pada elemen baris ke-1 pada kolom ke-1 memiliki persamaan yaitu :
- 9(x -1) – 7x = 1
- 9x – 9 – 7x = 1
- 2x = 10
- x = 5
Jadi, nilai x adalah = 5
Contoh Soal 17

Pembahasannya :
- 3A = 3

- 3A =

Jadi, nillai 3A adalah = 
Contoh Soal 18
Tentukan nilai x, y, dan z berikut ini, jika :

Penyelesaian :

Maka :
z = 1 ………………………………….……..(1)
–2y – 4x = –10
y + 2x = 5
y = 5 – 2x ..…………………………. (2)
6y + 2x = 3x + 4
6y + 2x – 3x = 4
6y – x = 4 …………………………… (3)
(2) akan disubtitusikan ke (3), sehingga menjadi :
6(5 – 2x) – x = 4
30 – 12x – x = 4
–13x = –26 maka x = 2
y = 5 – 2(2) = 1
z = 1
Contoh Soal 19
Diketahui matriks
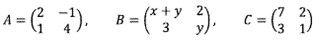
Apabila B − A = Ct = transpos matriks C, maka nilai x .y =….
A. 10
B. 15
C. 20
D. 25
E. 30
Pembahasannya :
Transpos C diperoleh dengan mengubah posisi baris ke kolom, B − A adalah pengurangan matriks B oleh A
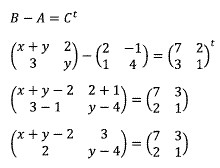
Akhirnya, dari kesamaan dua matriks:
y − 4 = 1
y = 5
x + y − 2 = 7
x + 5 − 2 = 7
x + 3 = 7
x = 4
x . y = (4)(5) = 20
Contoh Soal 20
Jika
![]()
maka x + y =….
A. − 15/4
B. − 9/4
C. 9/4
D. 15/4
E. 21/4
Pembahasannya :
Masih tentang kesamaan dua buah matriks ditambah tentang materi bentuk pangkat, mulai dari persamaan yang lebih mudah dulu:
3x − 2 = 7
3x = 7 + 2
3x = 9
x = 3
4x + 2y = 8
22(x + 2y) = 23
22x + 4y = 23
2x + 4y = 3
2(3) + 4y = 3
4y = 3 − 6
4y = − 3
y = − 3/4
Sehingga:
x + y = 3 + (− 3/4) = 2 1/4 = 9/4
Demikian pembahasan materi mengenai matriks. Semoga Bermanfaat dan dapat menambah wawasan kita. Terimakasih.
Daftar Pustaka:
https://www.ayokboco.com/matriks/
https://www.materi.carageo.com/pengertian-matriks/
https://blog.ruangguru.com/matematika-kelas-11-operasi-aljabar-pada-matriks-penjumlahan-
https://rumus.waheedbaly.com/contoh-soal-matriks-dan-jawabannya-kelas-11/
https://majalahpendidikan.com/soal-matriks-kelas-11/
https://rumus.co.id/contoh-soal-matriks/#Contoh_Soal_Matriks_Beserta_Pembahasannya
https://soalkimia.com/contoh-soal-matriks-determinan-dan-invers/


